Seno, cosseno e tangente: Difference between revisions
No edit summary Tag: wikieditor |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 16: | Line 16: | ||
Na geometria euclidiana a soma dos ângulos internos de um triângulo é 180°. Como um triângulo retângulo tem um ângulo de 90°, a soma dos outros dois sempre é 90° também. É por isso que não precisamos de regras ou propriedades para além de 90°, porque o restante dos ângulos apenas repetem ou espelham o que temos entre 0° e 90°. | Na geometria euclidiana a soma dos ângulos internos de um triângulo é 180°. Como um triângulo retângulo tem um ângulo de 90°, a soma dos outros dois sempre é 90° também. É por isso que não precisamos de regras ou propriedades para além de 90°, porque o restante dos ângulos apenas repetem ou espelham o que temos entre 0° e 90°. | ||
<math>\sen(\alpha) = \frac{BC}{AC}</math>. Significa quantas unidades estamos subindo (no eixo vertical) em relação a quantas unidades estamos andando para frente sobre a rampa. O que acontece com o ângulo nulo? Não subimos nada em relação a quantas unidades andamos para frente. Isto explica <math>\sen(0^{\text{o}}) = 0</math>. O que acontece com 90°? Aí temos uma razão 1:1, para cada unidade que andamos sobre a rampa, subimos da mesma distância em altura. Isto explica <math>\sen(90^{\text{o}}) = 1</math>. | <math>\text{sen}(\alpha) = \frac{BC}{AC}</math>. Significa quantas unidades estamos subindo (no eixo vertical) em relação a quantas unidades estamos andando para frente sobre a rampa. O que acontece com o ângulo nulo? Não subimos nada em relação a quantas unidades andamos para frente. Isto explica <math>\text{sen}(0^{\text{o}}) = 0</math>. O que acontece com 90°? Aí temos uma razão 1:1, para cada unidade que andamos sobre a rampa, subimos da mesma distância em altura. Isto explica <math>\text{sen}(90^{\text{o}}) = 1</math>. | ||
<math>\cos(\alpha) = \frac{AB}{AC}</math>. Significa quantas unidades estamos indo para frente em relação a quantidades unidades estamos percorrendo sobre a rampa. O que acontece com o ângulo nulo? Aí temos uma razão 1:1, para cada unidade da base que andamos para frente, percorremos a mesma distância sobre a rampa. Isto explica <math>\cos(0^{\text{o}}) = 1</math>. O que acontece com o ângulo de 90°? Aí não estamos andando para frente enquanto subimos. Isto explica <math>\cos(90^{\text{o}}) = 0</math>. | <math>\cos(\alpha) = \frac{AB}{AC}</math>. Significa quantas unidades estamos indo para frente em relação a quantidades unidades estamos percorrendo sobre a rampa. O que acontece com o ângulo nulo? Aí temos uma razão 1:1, para cada unidade da base que andamos para frente, percorremos a mesma distância sobre a rampa. Isto explica <math>\cos(0^{\text{o}}) = 1</math>. O que acontece com o ângulo de 90°? Aí não estamos andando para frente enquanto subimos. Isto explica <math>\cos(90^{\text{o}}) = 0</math>. | ||
| Line 26: | Line 26: | ||
Os professores se utilizam de diversos exemplos para mostrar as aplicações da trigonometria no mundo real: comprimento de sombras, altura de prédios, relógios solares, etc. A física tem muitos exemplos como jogar pedras na água num certo ângulo ou a reflexão da luz na superfície da água. Aqui não vou ficar dando todos os exemplos possíveis. | Os professores se utilizam de diversos exemplos para mostrar as aplicações da trigonometria no mundo real: comprimento de sombras, altura de prédios, relógios solares, etc. A física tem muitos exemplos como jogar pedras na água num certo ângulo ou a reflexão da luz na superfície da água. Aqui não vou ficar dando todos os exemplos possíveis. | ||
'''Trigonometria inversa:''' arco-seno, arco- | '''Trigonometria inversa:''' arco-seno, arco-cosseno e arco-tangente são as relações inversas às anteriores. Com seno, cosseno e tangente relacionamos o ângulo com a razão entre lados de um triângulo (retângulo). Com as relações trigonométricas inversas relacionamos a razão com o ângulo. | ||
'''Trigonometria recíproca:''' com todas as três relações trigonométricas fundamentais sendo razões, inverter a razão resulta na razão inversa. A confusão aqui é que as relações recíprocas, cosecante, cotangete e secante são razões invertidas, não a relação inversa entre ângulos e razões como na trigonometria inversa. | '''Trigonometria recíproca:''' com todas as três relações trigonométricas fundamentais sendo razões, inverter a razão resulta na razão inversa. A confusão aqui é que as relações recíprocas, cosecante, cotangete e secante são razões invertidas, não a relação inversa entre ângulos e razões como na trigonometria inversa. | ||
Latest revision as of 03:43, 15 February 2025
O padrão mais comum nas escolas é aprender primeiro a medir ângulos e como somar e subtrair ângulos. Depois vem a ideia do seno, cosseno e tangente. Uma pergunta é deixada sem resposta até aprendermos a definição do seno, cosseno e tangente.
A pergunta é: sabemos que uma rampa é mais ou menos difícil de subir dependendo do ângulo de inclinação, com zero sendo a menor dificuldade e 90° a máxima. Há alguma relação entre quantas unidades andamos para frente e quantas unidades estamos subindo em relação ao nível do solo numa rampa? Seno, cosseno e tangente são precisamente razões que relacionam ângulos com os lados de um triângulo de tal forma que temos como responder a questão anterior.
Note: ângulos não fazem sentido com menos do que duas dimensões.
Cuidado: sempre definimos a tangente, cosseno e seno com um triângulo retângulo. Se o triângulo não for retângulo as proporções relativas ao seno, cosseno e tangente não valem.
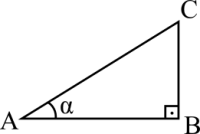 |
AB = base = afastamento BC = altura AC = rampa = hipotenusa |
Na geometria euclidiana a soma dos ângulos internos de um triângulo é 180°. Como um triângulo retângulo tem um ângulo de 90°, a soma dos outros dois sempre é 90° também. É por isso que não precisamos de regras ou propriedades para além de 90°, porque o restante dos ângulos apenas repetem ou espelham o que temos entre 0° e 90°.
[math]\displaystyle{ \text{sen}(\alpha) = \frac{BC}{AC} }[/math]. Significa quantas unidades estamos subindo (no eixo vertical) em relação a quantas unidades estamos andando para frente sobre a rampa. O que acontece com o ângulo nulo? Não subimos nada em relação a quantas unidades andamos para frente. Isto explica [math]\displaystyle{ \text{sen}(0^{\text{o}}) = 0 }[/math]. O que acontece com 90°? Aí temos uma razão 1:1, para cada unidade que andamos sobre a rampa, subimos da mesma distância em altura. Isto explica [math]\displaystyle{ \text{sen}(90^{\text{o}}) = 1 }[/math].
[math]\displaystyle{ \cos(\alpha) = \frac{AB}{AC} }[/math]. Significa quantas unidades estamos indo para frente em relação a quantidades unidades estamos percorrendo sobre a rampa. O que acontece com o ângulo nulo? Aí temos uma razão 1:1, para cada unidade da base que andamos para frente, percorremos a mesma distância sobre a rampa. Isto explica [math]\displaystyle{ \cos(0^{\text{o}}) = 1 }[/math]. O que acontece com o ângulo de 90°? Aí não estamos andando para frente enquanto subimos. Isto explica [math]\displaystyle{ \cos(90^{\text{o}}) = 0 }[/math].
[math]\displaystyle{ \tan(\alpha) = \frac{BC}{AB} }[/math]. Significa quantas unidades estamos subindo em relação a quantas unidades estamos indo para frente (na horizontal). O que acontece com o ângulo de 90°? A tangente não existe. Pense no círculo e num ponto no seu perímetro. Uma linha perpendicular (no mesmo plano do círculo) não pode ser tangente naquele ponto. É impossível ser tangente e perpendicular ao mesmo tempo. O que acontece com 45°? Aí temos uma razão 1:1, para cada unidade que subimos, estamos indo para frente da mesma distância. Isto explica [math]\displaystyle{ \tan(45^{\text{o}}) = 1 }[/math]. O que acontece com o ângulo nulo? Aí não subimos nada enquanto andamos para frente. É o mesmo que estar paralelo à direção seguida.
É bastante comum confundir seno e cosseno e por extensão, inverte os dois e confundir a tangente também. Na escola as pessoas se utilizam de piadas e trocadilhos para memorizar que o eixo horizontal é x e o vertical é y. Se você olhar o triângulo acima, o seno do ângulo sempre é o lado oposto dividido pelo comprimento da rampa. O cosseno é sempre o lado adjacente dividido pelo comprimento da rampa. A tangente é sempre altura / base. Eu acho que assim fica mais fácil memorizar que o seno sempre diz respeito à altura primeiro, enquanto o cosseno é a base primeiro. Portanto, a razão vertical / horizontal é a tangente.
Os professores se utilizam de diversos exemplos para mostrar as aplicações da trigonometria no mundo real: comprimento de sombras, altura de prédios, relógios solares, etc. A física tem muitos exemplos como jogar pedras na água num certo ângulo ou a reflexão da luz na superfície da água. Aqui não vou ficar dando todos os exemplos possíveis.
Trigonometria inversa: arco-seno, arco-cosseno e arco-tangente são as relações inversas às anteriores. Com seno, cosseno e tangente relacionamos o ângulo com a razão entre lados de um triângulo (retângulo). Com as relações trigonométricas inversas relacionamos a razão com o ângulo.
Trigonometria recíproca: com todas as três relações trigonométricas fundamentais sendo razões, inverter a razão resulta na razão inversa. A confusão aqui é que as relações recíprocas, cosecante, cotangete e secante são razões invertidas, não a relação inversa entre ângulos e razões como na trigonometria inversa.
Visualizando seno, cosseno e tangente como porcentagens
Outra forma de interpretar razões é como porcentagem, porque toda razão é uma porcentagem. Seno, cosseno e tangente variam entre 0 e 1, com os valores entre 0 e -1 sendo reflexões. Considere o diagrama acima que mostra [math]\displaystyle{ ||\overrightarrow{v}_x + \overrightarrow{v}_y|| = 1 }[/math]:
[math]\displaystyle{ \overrightarrow{v} \ \ = (0.866, 0.5) }[/math]
[math]\displaystyle{ \overrightarrow{v}_x = (0.866, 0) }[/math]
[math]\displaystyle{ \overrightarrow{v}_y = (0, 0.5) }[/math]
Quando temos uma quantidade escalar como tempo, massa ou dinheiro podemos subdividir em partes menores como 50% + 50% = 100%. Porém, com vetores não podemos fazer a mesma operação com velocidade, energia cinética ou deslocamento. A exceção é caso os vetores sejam paralelos entre si. Lembre-se que o seno, cosseno e tangente que calculamos são uma razão de comprimento / comprimento. Em física, quando fazemos uma razão de quantidades de mesma unidade, como m/s por m/s ou Newton por Newton, a unidade some.
No diagrama acima, 86.6% significa que se dividirmos a magnitude do vetor vertical pela magnitude da hipotenusa, concluímos que a vertical é 86.6% da hipotenusa. Em outras palavras, a vertical é menor do que a hipotenusa e jamais poderia ser maior por causa da desigualdade triangular. Outro ângulo, 45°. A tangente de 45° é 1, que corresponde a 100%. 100% do que? Tangente, por definição, é altura / base de um triângulo retângulo. 100% no caso de vetores significa que uma componente tem a mesma magnitude da outra. Não interprete como "magnitude total" do vetor resultante, como se cada componente representasse um % do vetor resultante.
Se o raciocínio anterior ainda estiver confuso, tente o seguinte: sen(60°) = 0.866 como mostrado. Para calculá-lo fazemos altura / hipotenusa. Não podemos usar seno ou cosseno para comparar o vetor vertical com o horizontal. Não vai dar certo. Seno e cosseno são quocientes entre a altura ou a base e a hipotenusa. Enquanto a tangente é entre altura e a base. Pensar que uma porcentagem, maior ou menor, representa uma parte de uma vetor só faz sentido se pensarmos em dois vetores paralelos. Como vamos comparar se a vertical é um certo % da horizontal ou vice-versa se, pela própria definição, seno e cosseno não são razões entre a componente horizontal e a vertical?
