Radianos: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
</div> | </div> | ||
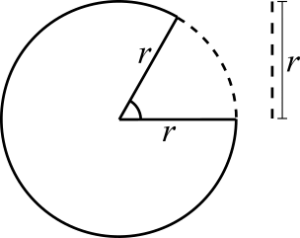
Um radiano é o ângulo no qual o comprimento de um arco do círculo é igual ao raio do mesmo. Quantas vezes o raio cabe no perímetro do círculo? Res: <math>2\pi</math> vezes para um raio igual a um. Isto é ~6.28...., um número real. | Um radiano é o ângulo no qual o comprimento de um arco do círculo é igual ao raio do mesmo. Quantas vezes o raio cabe no perímetro do círculo? Res: <math>2\pi</math> vezes para um raio igual a um. Isto é ~6.28...., um número real. <math>\pi</math> é igual à razão entre o perímetro e o diâmetro em qualquer circunferência. | ||
Se o perímetro de um círculo de raio um é <math>2\pi</math> e uma volta completa é 360°, aí esta a nossa fórmula de conversão entre radianos e graus. 180°, meia volta, é <math>\pi</math>. A partir daí fica fácil pensar em um quarto de ângulo, meio quarto e todos os valores múltiplos de voltas incompletas. Na maioria das vezes não precisamos de ângulos menores do que 30° ou maiores do que 180° nos exercícios. Podemos facilmente dividir um radiano por 10 ou cinco e obter múltiplos como 1° ou 25°. | Se o perímetro de um círculo de raio um é <math>2\pi</math> e uma volta completa é 360°, aí esta a nossa fórmula de conversão entre radianos e graus. 180°, meia volta, é <math>\pi</math>. A partir daí fica fácil pensar em um quarto de ângulo, meio quarto e todos os valores múltiplos de voltas incompletas. Na maioria das vezes não precisamos de ângulos menores do que 30° ou maiores do que 180° nos exercícios. Podemos facilmente dividir um radiano por 10 ou cinco e obter múltiplos como 1° ou 25°. | ||
Latest revision as of 00:26, 28 July 2022
Um radiano é o ângulo no qual o comprimento de um arco do círculo é igual ao raio do mesmo. Quantas vezes o raio cabe no perímetro do círculo? Res: [math]\displaystyle{ 2\pi }[/math] vezes para um raio igual a um. Isto é ~6.28...., um número real. [math]\displaystyle{ \pi }[/math] é igual à razão entre o perímetro e o diâmetro em qualquer circunferência.
Se o perímetro de um círculo de raio um é [math]\displaystyle{ 2\pi }[/math] e uma volta completa é 360°, aí esta a nossa fórmula de conversão entre radianos e graus. 180°, meia volta, é [math]\displaystyle{ \pi }[/math]. A partir daí fica fácil pensar em um quarto de ângulo, meio quarto e todos os valores múltiplos de voltas incompletas. Na maioria das vezes não precisamos de ângulos menores do que 30° ou maiores do que 180° nos exercícios. Podemos facilmente dividir um radiano por 10 ou cinco e obter múltiplos como 1° ou 25°.