Discussão informal da constante de Euler: Difference between revisions
No edit summary |
No edit summary Tag: wikieditor |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
</div> | </div> | ||
Eu vou usar o conceito da '''integral''' sem o formalismo. Se você derivar o '''logaritmo natural''' o resultado é o inverso de <math>x</math>. A outra direção, se você calcular a '''área debaixo | Eu vou usar o conceito da '''integral''' sem o formalismo. Se você derivar o '''logaritmo natural''' o resultado é o inverso de <math>x</math>. A outra direção, se você calcular a '''área debaixo da curva da função''' dada pelo inverso de <math>x</math>, resulta no logaritmo natural. A razão para esta função específica, <math>f(x) = 1/x</math>, é porque a derivada de um log numa base que não seja <math>e</math> resulta em <math>1/(xb)</math>. Onde <math>b \neq 1</math> e é algum logaritmo. Com o log natural temos que <math>\ln(e) = 1 \iff e^1 = e</math>, o que implica que integrando <math>1/x</math> de 1 até <math>e</math> o resultado é 1. Por quê integrar a partir de 1? Porque <math>e^0 = 1 \iff \ln(1) = 0</math>. Por hora é suficiente dizer que o conceito da integral que aprendemos inicialmente é um somatório de áreas de retângulos embaixo da curva da função. A base do retângulo é <math>x_2 - x_1</math> e a altura é <math>f(x_2)</math>. Há uma questão de erro associada ao computo de uma pequena área entre o retângulo e a função, mas estou ignorando o formalismo da '''Integral de Riemann''' por hora. | ||
Você pode tentar calcular a área debaixo de <math>1/x</math>, de 1 até <math>e</math>, com uma calculadora e força bruta. Tente um retângulo cuja base seja <math>1.2 - 1.1</math> e a altura seja <math>f(1.2)</math>. Some a área deste com mais um retângulo, agora de base <math>1.3 - 1.2</math> e altura igual a <math>f(1.3)</math>. Repita até você chegar num valor menor do que 1 e próximo a este. Se deformarmos o gráfico de <math>1/x</math> por meio de uma multiplicação por uma constante <math>c > 0</math> e <math>c \neq 1</math>, a área de 1 até <math>e</math> não será igual a 1. Isto também implica que <math>c \cdot \ln(e) \neq 1</math>. Se fizermos uma composição, aplicando <math>g(x)</math> para deformar o gráfico de <math>1/x</math>, também estaremos mudando a área de 1 até <math>e</math>. | Você pode tentar calcular a área debaixo de <math>1/x</math>, de 1 até <math>e</math>, com uma calculadora e força bruta. Tente um retângulo cuja base seja <math>1.2 - 1.1</math> e a altura seja <math>f(1.2)</math>. Some a área deste com mais um retângulo, agora de base <math>1.3 - 1.2</math> e altura igual a <math>f(1.3)</math>. Repita até você chegar num valor menor do que 1 e próximo a este. Se deformarmos o gráfico de <math>1/x</math> por meio de uma multiplicação por uma constante <math>c > 0</math> e <math>c \neq 1</math>, a área de 1 até <math>e</math> não será igual a 1. Isto também implica que <math>c \cdot \ln(e) \neq 1</math>. Se fizermos uma composição, aplicando <math>g(x)</math> para deformar o gráfico de <math>1/x</math>, também estaremos mudando a área de 1 até <math>e</math>. | ||
| Line 11: | Line 11: | ||
Uma maneira formal de definir <math>e</math> requer o cálculo do limite de uma sequência. Vamos pular a teoria por hora. Calcular a soma da área de retângulos é o equivalente a somar números. Com isto em mente deve haver uma soma de números tal que o resultado seja <math>e</math>. Sim, é esta aqui: | Uma maneira formal de definir <math>e</math> requer o cálculo do limite de uma sequência. Vamos pular a teoria por hora. Calcular a soma da área de retângulos é o equivalente a somar números. Com isto em mente deve haver uma soma de números tal que o resultado seja <math>e</math>. Sim, é esta aqui: | ||
<math>\ | <math>e = \sum\limits_{n = 0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + \cdots.</math> | ||
[[category:Teoria_do_Cálculo]] | |||
Latest revision as of 15:36, 12 November 2025
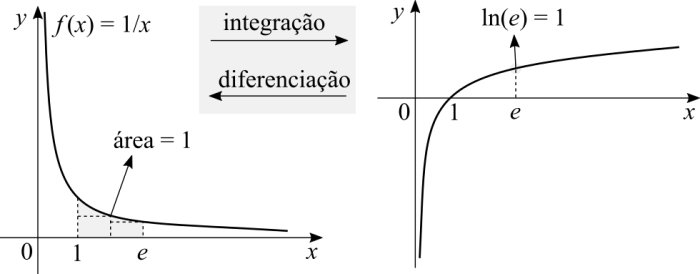
Eu vou usar o conceito da integral sem o formalismo. Se você derivar o logaritmo natural o resultado é o inverso de [math]\displaystyle{ x }[/math]. A outra direção, se você calcular a área debaixo da curva da função dada pelo inverso de [math]\displaystyle{ x }[/math], resulta no logaritmo natural. A razão para esta função específica, [math]\displaystyle{ f(x) = 1/x }[/math], é porque a derivada de um log numa base que não seja [math]\displaystyle{ e }[/math] resulta em [math]\displaystyle{ 1/(xb) }[/math]. Onde [math]\displaystyle{ b \neq 1 }[/math] e é algum logaritmo. Com o log natural temos que [math]\displaystyle{ \ln(e) = 1 \iff e^1 = e }[/math], o que implica que integrando [math]\displaystyle{ 1/x }[/math] de 1 até [math]\displaystyle{ e }[/math] o resultado é 1. Por quê integrar a partir de 1? Porque [math]\displaystyle{ e^0 = 1 \iff \ln(1) = 0 }[/math]. Por hora é suficiente dizer que o conceito da integral que aprendemos inicialmente é um somatório de áreas de retângulos embaixo da curva da função. A base do retângulo é [math]\displaystyle{ x_2 - x_1 }[/math] e a altura é [math]\displaystyle{ f(x_2) }[/math]. Há uma questão de erro associada ao computo de uma pequena área entre o retângulo e a função, mas estou ignorando o formalismo da Integral de Riemann por hora.
Você pode tentar calcular a área debaixo de [math]\displaystyle{ 1/x }[/math], de 1 até [math]\displaystyle{ e }[/math], com uma calculadora e força bruta. Tente um retângulo cuja base seja [math]\displaystyle{ 1.2 - 1.1 }[/math] e a altura seja [math]\displaystyle{ f(1.2) }[/math]. Some a área deste com mais um retângulo, agora de base [math]\displaystyle{ 1.3 - 1.2 }[/math] e altura igual a [math]\displaystyle{ f(1.3) }[/math]. Repita até você chegar num valor menor do que 1 e próximo a este. Se deformarmos o gráfico de [math]\displaystyle{ 1/x }[/math] por meio de uma multiplicação por uma constante [math]\displaystyle{ c \gt 0 }[/math] e [math]\displaystyle{ c \neq 1 }[/math], a área de 1 até [math]\displaystyle{ e }[/math] não será igual a 1. Isto também implica que [math]\displaystyle{ c \cdot \ln(e) \neq 1 }[/math]. Se fizermos uma composição, aplicando [math]\displaystyle{ g(x) }[/math] para deformar o gráfico de [math]\displaystyle{ 1/x }[/math], também estaremos mudando a área de 1 até [math]\displaystyle{ e }[/math].
Uma maneira formal de definir [math]\displaystyle{ e }[/math] requer o cálculo do limite de uma sequência. Vamos pular a teoria por hora. Calcular a soma da área de retângulos é o equivalente a somar números. Com isto em mente deve haver uma soma de números tal que o resultado seja [math]\displaystyle{ e }[/math]. Sim, é esta aqui:
[math]\displaystyle{ e = \sum\limits_{n = 0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + \cdots. }[/math]