Aproximação linear para uma variável: Difference between revisions
(Created page with "A maioria dos livros explicam o problema de achar a reta tangente num certo ponto de uma função. A ideia geométrica por trás da derivada é a de que, se a função for diferenciável, então podemos aproximá-la por uma função linear. Alguns livros dão a ideia de ampliar a imagem como um microscópio faz para ver coisas muito pequenas. Quando dois pontos da função são muito próximos um do outro podemos considerar uma taxa de variação média entre eles. Numer...") |
No edit summary Tag: wikieditor |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
Com cálculo sempre traçamos gráficos num espaço euclidiano. Na geometria euclidiana a menor distância entre dois pontos sempre é uma linha reta. Esta é uma forma de explicar porque temos o problema de achar a reta tangente. Entre dois pontos temos infinitos caminhos, mas apenas um, uma linha reta é o que minimiza a distância percorrida. Nem todo professor menciona a geometria euclidiana e há ainda o problema de tempo. Nem sempre o tempo é suficiente para passar todos os detalhes. | |||
<div style="text-align:center;"> | <div style="text-align:center;"> | ||
| Line 15: | Line 14: | ||
</div> | </div> | ||
Esta claro que a reta tangente é uma boa aproximação da função se considerarmos uma certa margem de erro. O gráfico claramente mostra que além de uma certa margem de erro o erro é grande demais. Uma maneira de pensar sobre isto é considerar a dificuldade de calcularmos o valor da função. Dependendo do caso pode ser aceitável trocar a função por uma aproximação linear, o que torna o cálculo mais simples e rápido. Em aulas de métodos numéricos temos um discussão mais aprofundada sobre o tema porque queremos responder à pergunta ''"Quão próximo precisamos chegar do valor verdadeiro? Há um limite para o erro?"'' | |||
Com a geometria analítica podemos achar equações da reta se conhecermos dois pontos ou um ponto e um coeficiente angular. O mesmo conceito se aplica para achar funções que passam por pontos. Com a definição da derivada podemos achar uma função afim que aproxima uma função com uma simples manipulação algébrica: | |||
<math>\frac{f(x) - f(p)}{x - p} = f'(p)</math> | <math>\frac{f(x) - f(p)}{x - p} = f'(p)</math> | ||
<math>f(x) = f(p) + f'(p)(x - p)</math> ''( | <math>f(x) = f(p) + f'(p)(x - p)</math> ''(Lembre-se que <math>x - p \neq 0</math>)'' | ||
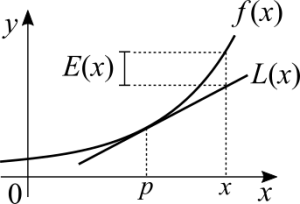
Observe que no gráfico acima existe um <math>E(x)</math> que representa a diferença entre a função afim e a função que estamos aproximando. Portanto: | |||
<math>L(x) = f(p) + f'(p)(x - p) + E(x)</math> | <math>L(x) = f(p) + f'(p)(x - p) + E(x)</math> | ||
A melhor aproximação neste caso ocorre quando <math>E(x) = 0</math>. Ou seja, estamos o mais próximo possível da função que estamos aproximando. | |||
Nem toda função será mais fácil de calcular desta forma. Primeiro há o problema da diferenciabilidade. Se a função não for diferenciável não podemos usar a aproximação linear. Segundo, trocar um seno por cosseno ou vice-versa não ajuda nem atrapalha. | |||
[[category:Teoria_do_Cálculo]] | |||
Latest revision as of 15:39, 12 November 2025
A maioria dos livros explicam o problema de achar a reta tangente num certo ponto de uma função. A ideia geométrica por trás da derivada é a de que, se a função for diferenciável, então podemos aproximá-la por uma função linear. Alguns livros dão a ideia de ampliar a imagem como um microscópio faz para ver coisas muito pequenas. Quando dois pontos da função são muito próximos um do outro podemos considerar uma taxa de variação média entre eles. Numericamente significa aceitar uma margem de erro em troca de perdermos precisão ao considerarmos uma função mais simples entre dois pontos, a fim de simplificar cálculos. No caso da reta tangente o que se tem é, que entre dois pontos, podemos considerar uma taxa de variação constante.
Com cálculo sempre traçamos gráficos num espaço euclidiano. Na geometria euclidiana a menor distância entre dois pontos sempre é uma linha reta. Esta é uma forma de explicar porque temos o problema de achar a reta tangente. Entre dois pontos temos infinitos caminhos, mas apenas um, uma linha reta é o que minimiza a distância percorrida. Nem todo professor menciona a geometria euclidiana e há ainda o problema de tempo. Nem sempre o tempo é suficiente para passar todos os detalhes.
Esta claro que a reta tangente é uma boa aproximação da função se considerarmos uma certa margem de erro. O gráfico claramente mostra que além de uma certa margem de erro o erro é grande demais. Uma maneira de pensar sobre isto é considerar a dificuldade de calcularmos o valor da função. Dependendo do caso pode ser aceitável trocar a função por uma aproximação linear, o que torna o cálculo mais simples e rápido. Em aulas de métodos numéricos temos um discussão mais aprofundada sobre o tema porque queremos responder à pergunta "Quão próximo precisamos chegar do valor verdadeiro? Há um limite para o erro?"
Com a geometria analítica podemos achar equações da reta se conhecermos dois pontos ou um ponto e um coeficiente angular. O mesmo conceito se aplica para achar funções que passam por pontos. Com a definição da derivada podemos achar uma função afim que aproxima uma função com uma simples manipulação algébrica:
[math]\displaystyle{ \frac{f(x) - f(p)}{x - p} = f'(p) }[/math]
[math]\displaystyle{ f(x) = f(p) + f'(p)(x - p) }[/math] (Lembre-se que [math]\displaystyle{ x - p \neq 0 }[/math])
Observe que no gráfico acima existe um [math]\displaystyle{ E(x) }[/math] que representa a diferença entre a função afim e a função que estamos aproximando. Portanto:
[math]\displaystyle{ L(x) = f(p) + f'(p)(x - p) + E(x) }[/math]
A melhor aproximação neste caso ocorre quando [math]\displaystyle{ E(x) = 0 }[/math]. Ou seja, estamos o mais próximo possível da função que estamos aproximando.
Nem toda função será mais fácil de calcular desta forma. Primeiro há o problema da diferenciabilidade. Se a função não for diferenciável não podemos usar a aproximação linear. Segundo, trocar um seno por cosseno ou vice-versa não ajuda nem atrapalha.