Polar coordinates: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
The '''Cartesian system of coordinates''', or rectangular | The '''Cartesian system of coordinates''', or rectangular coordinates, is the most widely known because it's the most common. We subdivide the plane with columns and rows and each position is located by knowing the column and row. At school most people should have had a teacher who compared the Cartesian system with the game Battleship or a chessboard. | ||
The Cartesian system is easier to understand because in it we have left and right, up and down, exactly as in daily life. There is another system of coordinates called '''Polar Coordinates''' that locates points with two coordinates: '''angle''' and '''distance'''. If we add a second angle to the Polar system we get the Spherical system for 3D. | The Cartesian system is easier to understand because in it we have left and right, up and down, exactly as in daily life. It's natural to think in terms of North - South, West - East directions. There is another system of coordinates called '''Polar Coordinates''' that locates points with two coordinates: '''angle''' and '''distance'''. If we add a second angle to the Polar system we get the Spherical system for 3D. | ||
Going beyond and we can naturally extend the Cartesian and Spherical coordinate systems to even higher dimensions. A 4D space has four linearly independent axis, but we cannot draw or see it. | Going beyond and we can naturally extend the Cartesian and Spherical coordinate systems to even higher dimensions. A 4D space has four linearly independent axis, but we cannot draw or see it. | ||
| Line 12: | Line 12: | ||
There is one important fact that relates both coordinate systems, Polar and Cartesian. Each point has a unique location in the space and this fact is what makes it possible to overlap both systems. Each point can have its position described by both systems at the same time. | There is one important fact that relates both coordinate systems, Polar and Cartesian. Each point has a unique location in the space and this fact is what makes it possible to overlap both systems. Each point can have its position described by both systems at the same time. | ||
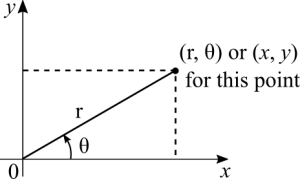
The most common mistake is to confuse Cartesian with polar when plotting a graph. For example: everyone is familiar with '''(x, y)'''. Therefore a common mistake is to think that radius goes along '''x''' and angle is somewhere along '''y'''. Suppose we have (2, 45°). A clueless person thinks x = 2 and y = 45. I have to admit here that I made this mistake and more than once. I think that the origin of this mistake is, ironically, the fact that, a lot of times, polar coordinates are overlapped with the Cartesian coordinates in the same way that the figure above shows. This is done mostly due to the fact that it's easier to think on distances with XY coordinates. | |||
In linear algebra we learn the concept of linear dependency and with it we learn that as long as we have two linearly independent vectors, the coordinate system of a plane or space if we have a third vector, doesn't have to be rectangular. One axis can very well be angled. We just don't see such coordinate system very often because the fact that the axes are perpendicular to each other makes our lives easier. The unit circle and the dot product really depend on the fact that the axis are perpendicular to each other. | |||
==Conversion between Polar and Cartesian systems== | |||
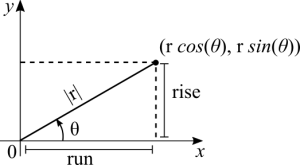
Let's take a look at the same figure, but now with attention to sine and cosine ''(I'm assuming that you know how to read the unit circle)'': | |||
<div style="text-align:center;"> | |||
[[file:polar_system_conversion.png|300px]] | |||
</div> | |||
'''Conversion from Polar to Cartesian:''' | |||
<math>\sin(\theta) = \frac{\text{rise}}{r} \iff r \sin(\theta) = \text{rise}</math> | |||
<math>\cos(\theta) = \frac{\text{run}}{r} \iff r \cos(\theta) = \text{run}</math> | |||
''(Careful! The division by the radius is allowed because we are considering that the distance is never negative nor null. The Cartesian coordinates themselves can be negative numbers, but a distance is never negative.)'' | |||
The reverse process, from Cartesian to Polar, has an added complexity caused by some issues related to angles. | |||
Revision as of 18:01, 26 January 2022
The Cartesian system of coordinates, or rectangular coordinates, is the most widely known because it's the most common. We subdivide the plane with columns and rows and each position is located by knowing the column and row. At school most people should have had a teacher who compared the Cartesian system with the game Battleship or a chessboard.
The Cartesian system is easier to understand because in it we have left and right, up and down, exactly as in daily life. It's natural to think in terms of North - South, West - East directions. There is another system of coordinates called Polar Coordinates that locates points with two coordinates: angle and distance. If we add a second angle to the Polar system we get the Spherical system for 3D.
Going beyond and we can naturally extend the Cartesian and Spherical coordinate systems to even higher dimensions. A 4D space has four linearly independent axis, but we cannot draw or see it.
There is one important fact that relates both coordinate systems, Polar and Cartesian. Each point has a unique location in the space and this fact is what makes it possible to overlap both systems. Each point can have its position described by both systems at the same time.
The most common mistake is to confuse Cartesian with polar when plotting a graph. For example: everyone is familiar with (x, y). Therefore a common mistake is to think that radius goes along x and angle is somewhere along y. Suppose we have (2, 45°). A clueless person thinks x = 2 and y = 45. I have to admit here that I made this mistake and more than once. I think that the origin of this mistake is, ironically, the fact that, a lot of times, polar coordinates are overlapped with the Cartesian coordinates in the same way that the figure above shows. This is done mostly due to the fact that it's easier to think on distances with XY coordinates.
In linear algebra we learn the concept of linear dependency and with it we learn that as long as we have two linearly independent vectors, the coordinate system of a plane or space if we have a third vector, doesn't have to be rectangular. One axis can very well be angled. We just don't see such coordinate system very often because the fact that the axes are perpendicular to each other makes our lives easier. The unit circle and the dot product really depend on the fact that the axis are perpendicular to each other.
Conversion between Polar and Cartesian systems
Let's take a look at the same figure, but now with attention to sine and cosine (I'm assuming that you know how to read the unit circle):
Conversion from Polar to Cartesian:
[math]\displaystyle{ \sin(\theta) = \frac{\text{rise}}{r} \iff r \sin(\theta) = \text{rise} }[/math]
[math]\displaystyle{ \cos(\theta) = \frac{\text{run}}{r} \iff r \cos(\theta) = \text{run} }[/math]
(Careful! The division by the radius is allowed because we are considering that the distance is never negative nor null. The Cartesian coordinates themselves can be negative numbers, but a distance is never negative.)
The reverse process, from Cartesian to Polar, has an added complexity caused by some issues related to angles.