Implicit differentiation

An explicitly defined function is of the form [math]\displaystyle{ y = f(x) }[/math], such as [math]\displaystyle{ f(x) = x^2 + 2 }[/math]. An implicitly defined function does not present the variables neatly to the right and to the left. For example: [math]\displaystyle{ x^2 + y^2 = 4 }[/math]. It's not an equation of a function, it describes a circle according to analytical geometry. However, it does "hide" a function in it. We can isolate [math]\displaystyle{ y }[/math] to obtain [math]\displaystyle{ y = \pm \sqrt{x^2 + 1} }[/math]. Due to the circle being symmetric in all directions we could have isolated [math]\displaystyle{ x }[/math] to obtain the same equation, except that we'd have swapped the variables.

For complicated equations such as [math]\displaystyle{ y^3 + x^2y^2 + 4x = 0 }[/math] we can try, but it's going to be almost impossible to properly isolate the variable and find the explicit function. A graphical way to interpret such equations is to think on them in terms of analytical geometry. How many [math]\displaystyle{ (x, \ y) }[/math] pairs satisfy the previously mentioned equation? Infinitely many, it's an equation that in 2D describes some curve or path. In the same way we can plot functions point by point and connecting them with straight lines, a complicated curve can also be approximated with the same procedure.

The previous given curve could be rewritten as [math]\displaystyle{ [f(x)]^3 + x^2[f(x)]^2 + 4x = 0 }[/math] if we remember that [math]\displaystyle{ y = f(x) }[/math]. There is a function that we don't know, but the substitution made it clear that there is a relationship between the two variables. With calculus we can't solve that equation and there are probably multiple functions that would satisfy it. What we can do is to find the derivative of [math]\displaystyle{ f }[/math] and with that get a better idea of the curve's shape.

The same reasoning can be extended to multivariable functions.

Practical discussion

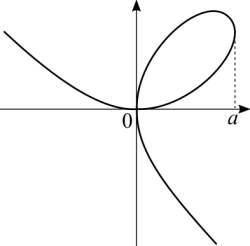
The previous discussion may have been too abstract. Let's discuss the Folium of Descartes:

[math]\displaystyle{ x^3 + y^3 = 3xy }[/math]

The graph can be described by a function, but it has to be a piecewise function. For the interval [math]\displaystyle{ [0,a] }[/math] we have that a certain [math]\displaystyle{ x }[/math] can correspond to up to three different values for [math]\displaystyle{ y }[/math]. This means that in that interval there are up to three different functions. It makes perfect sense since the equation has [math]\displaystyle{ y^3 }[/math] which accepts up to three values.

If we think about the function that can trace that graph and the problem of finding the tangent line on a given point, we have to think on [math]\displaystyle{ y' = f'(x) }[/math]. We have an equation and derive both sides in respect to the same variable. Using the Leibniz's notation:

[math]\displaystyle{ \frac{d}{dx}x^3 + \frac{d}{dx}y^3 = \frac{d}{dx}(3xy) }[/math] (we already began with the property of the sum of derivatives)

[math]\displaystyle{ 3x^2 + \frac{d}{dx}y^3 = 3y + 3x\frac{dy}{dx} }[/math] (the first derivative is easy. The right side is a product of two functions. [math]\displaystyle{ 3x }[/math] is explicit and [math]\displaystyle{ y }[/math] is some unknown function. Therefore, use the product rule. Don't confuse with partial derivatives)

[math]\displaystyle{ 3x^2 + 3y^2\frac{dy}{dx} = 3y + 3x\frac{dy}{dx} }[/math] (the derivative of [math]\displaystyle{ y^3 }[/math] is [math]\displaystyle{ 3y^2 }[/math] but it's a composite function, it has to be multiplied by [math]\displaystyle{ y' }[/math]. If you didn't grasp it, try this [math]\displaystyle{ f(y) = y^3 }[/math]. [math]\displaystyle{ g(y) = \ ? }[/math]. Then [math]\displaystyle{ f(g(y)) = \ ?^3 }[/math]. We don't know [math]\displaystyle{ g }[/math] but that doesn't prevent us from knowing how to derive [math]\displaystyle{ f }[/math]. [math]\displaystyle{ (f \circ g)' = 3g^2 g' }[/math])

[math]\displaystyle{ x^2 + y^2\frac{dy}{dx} = y + x\frac{dy}{dx} }[/math] (divide everything by 3)

[math]\displaystyle{ y^2\frac{dy}{dx} - x\frac{dy}{dx} = y - x^2 }[/math] (rearranged)

[math]\displaystyle{ \frac{dy}{dx}(y^2 - x) = y - x^2 }[/math] (factor out the derivative)

[math]\displaystyle{ \frac{dy}{dx} = \frac{y - x^2}{y^2 - x} }[/math] (we are not considering the origin)