Extreme values of a function: Difference between revisions
(Created page with "If a function is not constant a natural question is whether the function has a maximum value or a minimum value. In calculus we aren't concerned with physical barriers such as temperature going below zero kelvin or speed going beyond the speed of light. The function can have points where the maximum or minimum is local or global. It's important to say that when the limit at a point results in infinity, that point cannot be a maximum or minimum because infinity is not a n...") |
No edit summary |
||
| Line 1: | Line 1: | ||
If a function is not constant a natural question is whether the function has a maximum value or a minimum value. In calculus we aren't concerned with physical barriers such as temperature going below zero kelvin or speed going beyond the speed of light. The function can have points where the maximum or minimum is local or global. It's important to say that when the limit at a point results in infinity, that point cannot be a maximum or minimum because infinity is not a number that can be reached. | If a function is not constant a natural question is whether the function has a maximum value or a minimum value. In calculus we aren't concerned with physical barriers such as temperature going below zero kelvin or speed going beyond the speed of light. The function can have points where the maximum or minimum is local or global. It's important to say that when the limit at a point results in infinity, that point cannot be a maximum or minimum because infinity is not a number that can be reached. A function may be strictly crescent or decrescent such that maximum points don't exist anywhere in its domain. | ||
<div style="text-align:center;> | |||
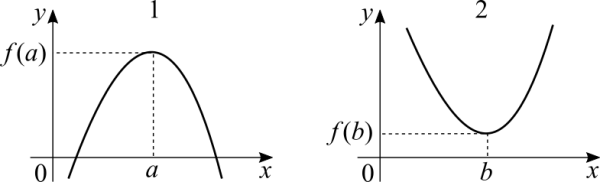
[[file:extreme_values_graph.png|600px]] | |||
</div> | |||
Case 1: <math>(a, \ f(a))</math> is an '''absolute maximum''' of <math>f</math> because <math>f(a) \geq f(x)</math> for all <math>x \in D_f</math>.<br />Case 2: <math>(b, \ f(b))</math> is an '''absolute minimum''' of <math>f</math> because <math>f(b) \leq f(x)</math> for all <math>x \in D_f</math>. | |||
The maximum and minimum values of <math>f</math> are called '''extreme values''' of <math>f</math>. | |||
'''Absolute''' and '''global''' mean the same thing, but maybe the word "absolute" can cause some confusion related to the '''absolute value'''. | |||
'''Note:''' sometimes the zero of a function coincides with a maximum or a minimum, but that's not always the case. | |||
Revision as of 21:02, 21 March 2022
If a function is not constant a natural question is whether the function has a maximum value or a minimum value. In calculus we aren't concerned with physical barriers such as temperature going below zero kelvin or speed going beyond the speed of light. The function can have points where the maximum or minimum is local or global. It's important to say that when the limit at a point results in infinity, that point cannot be a maximum or minimum because infinity is not a number that can be reached. A function may be strictly crescent or decrescent such that maximum points don't exist anywhere in its domain.
Case 1: [math]\displaystyle{ (a, \ f(a)) }[/math] is an absolute maximum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(a) \geq f(x) }[/math] for all [math]\displaystyle{ x \in D_f }[/math].
Case 2: [math]\displaystyle{ (b, \ f(b)) }[/math] is an absolute minimum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(b) \leq f(x) }[/math] for all [math]\displaystyle{ x \in D_f }[/math].
The maximum and minimum values of [math]\displaystyle{ f }[/math] are called extreme values of [math]\displaystyle{ f }[/math].
Absolute and global mean the same thing, but maybe the word "absolute" can cause some confusion related to the absolute value.
Note: sometimes the zero of a function coincides with a maximum or a minimum, but that's not always the case.