Extreme values of a function

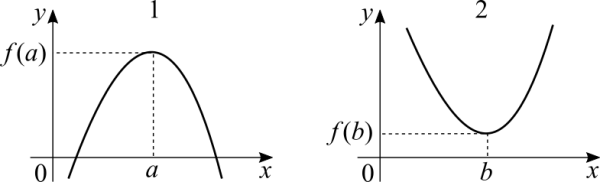
If a function is not constant a natural question is whether the function has a maximum value or a minimum value. In calculus we aren't concerned with physical barriers such as temperature going below zero kelvin or speed going beyond the speed of light. The function can have points where the maximum or minimum is local or global. It's important to say that when the limit at a point results in infinity, that point cannot be a maximum or minimum because infinity is not a number that can be reached.

Case 1: [math]\displaystyle{ (a, \ f(a)) }[/math] is an absolute maximum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(a) \geq f(x) }[/math] for all [math]\displaystyle{ x \in D_f }[/math].
Case 2: [math]\displaystyle{ (b, \ f(b)) }[/math] is an absolute minimum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(b) \leq f(x) }[/math] for all [math]\displaystyle{ x \in D_f }[/math].

The maximum and minimum values of [math]\displaystyle{ f }[/math] are called extreme values of [math]\displaystyle{ f }[/math]. In case the function is strictly crescent or strictly decrescent, extreme values don't exist.

Absolute maximum and global maximum mean the same thing, but maybe the word "absolute" can cause some confusion related to the absolute value.

Note: sometimes the zero of a function coincides with a maximum or a minimum, but that's not always the case.

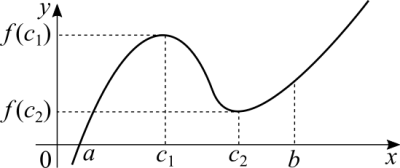
If we restrict out analysis to a sub-interval of the function's domain we have local maximum or minimum points. They may coincide with the global maximum or minimum, but that's not always the case. From 0 to e:

[math]\displaystyle{ (c, \ f(c)) }[/math] is a local maximum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(c) \geq f(x) }[/math] for all [math]\displaystyle{ x \in ]0, \ e[ }[/math].
[math]\displaystyle{ (d, \ f(d)) }[/math] is a local minimum of [math]\displaystyle{ f }[/math] because [math]\displaystyle{ f(d) \leq f(x) }[/math] for all [math]\displaystyle{ x \in ]c, \ e[ }[/math].

The reason for an open interval is because the limit at the extremes may not exist, meaning that the function is discontinuous there. If the limit is infinity, it can't be a maximum or a minimum because we can't regard infinity as a number. In case the limit does exist but the function is undefined there, we can keep finding values closer and closer to that limit without ever reaching it. Which means that for every maximum or minimum value that we find there is another and another, endlessly. The local maximum or minimum must be somewhere in between the two extremes, except for the extreme values themselves. The sub-interval is arbitrary, there is no special theory to define it.

If you noticed, the examples are closely related to the Rolle's theorem, because the maximum and minimum points coincide with the point where [math]\displaystyle{ f'(x) = 0 }[/math]. That's not always the case though. If the function is strictly crescent or decrescent and we choose a sub-interval of its domain, the maximum and minimum values are obviously going to be the extremes of the interval.

In Calculus we are unable to prove the Weierstrass theorem of extreme values because it requires knowledge that is beyond calculus. But we can use it to study the behaviour of functions. If a function is continuous and constant in an interval, maximum and minimum are equal to each other. Else, if the function is non-constant, it's pretty natural to assume that there must be a highest and a lowest point in that interval.

Think about the meaning of the derivative. It's a function that represents the rate of change of another function. If the rate of change is always increasing or always decreasing, then the function does not change its rate of change and cannot have a global maximum or a global minimum. Else, if the rate of change inverts its sign somewhere, then it must be equal to zero somewhere in the interval we are doing our analysis. What I just explained is the idea of finding the roots of the derivative itself.

When we have a function given by some equation that we know how to solve, such as an polynomial equation, finding the roots doesn't always coincide with finding maximum or minimum points. But it does give us the information about the function assuming positive or negative values before or after the root. By knowing that we can know whether the function is increasing or decreasing near the root.

The first two tools that we have to study the behaviour of functions is calculating roots of equations and derivatives, specially the roots of the derivative itself.

The idea of finding the roots of the derivative can be extended to functions of many variables. The analysis becomes more complicated though because even if each partial derivative is equal to zero at a point, in one variable the function may be increasing while in the other it's decreasing. In additions, roots of functions of many variables aren't a single point, but whole intersections between surfaces and the XY plane (beyond 3D we can't even have graphical representations).