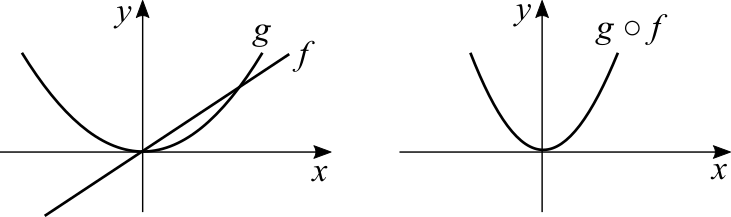Chain rule for single variable functions: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
The chain rule is, intuitively, a product of two derivatives. Suppose | The chain rule is, intuitively, a product of two derivatives. Suppose we have three moving things: A, B and C and their respective speeds are A > B > C. If we know how many times the speed of A is in comparison to B and B in comparison to C, then we can know how many times A is in comparison to C too. What we have to do is to multiply the ratios between A and B and between B and C. This is the example in [https://en.wikipedia.org/wiki/Chain_rule Wikipedia's article]. | ||
Another example. In meteorology there is the [https://en.wikipedia.org/wiki/Lapse_rate Lapse rate] which is the variation in temperature according to how high we are in the atmosphere. To make calculations easier during classes what most teachers do is to use the ratio 10 °C per km. Which means that for every 1 km that we go up in the atmosphere, the temperature should decrease by 10 °C. If we fly up or down we experience changes in temperature because we are moving in respect to each level of temperature in the atmosphere. The other way around doesn't happen because if we stay put the atmosphere won't move up or down in respect to us. Flying faster naturally yields a faster change in temperature. The atmosphere has its own rate temperature / height and we, by flying up or down, also have a rate of change of temperature / height. Doing the product of the two should yield the rate of change of temperature over time. | |||
<div style="text-align:center;> | <div style="text-align:center;> | ||
| Line 7: | Line 7: | ||
</div> | </div> | ||
The definition of a function states that we have one variable that depends upon another. In the case of composite functions, the value of one function depends on the value of the other function. | The definition of a function states that we have one variable that depends upon another. In the case of composite functions, the value of one function depends on the value of the other function. | ||
<div style="text-align:center;> | <div style="text-align:center;> | ||
| Line 16: | Line 16: | ||
'''Note:''' sometimes we have composite functions but we don't see them clearly. For example: <math>y = \sin^2(x)</math>. We can see that we have a product <math>y = \sin(x) \sin(x)</math>, but we could also see it as <math>y = x^2</math> and <math>x = sin(x)</math>. In a more conventional notation: <math>f(x) = x^2</math>, and <math>g(x) = \sin(x)</math> and <math>f \circ g = \sin^2(x)</math>. This is specially common with implicit differentiation. | '''Note:''' sometimes we have composite functions but we don't see them clearly. For example: <math>y = \sin^2(x)</math>. We can see that we have a product <math>y = \sin(x) \sin(x)</math>, but we could also see it as <math>y = x^2</math> and <math>x = sin(x)</math>. In a more conventional notation: <math>f(x) = x^2</math>, and <math>g(x) = \sin(x)</math> and <math>f \circ g = \sin^2(x)</math>. This is specially common with implicit differentiation. | ||
'''Wrong reasoning:''' I'm leaving this here. It's a previous explanation that I had that is confusing and may still serve a purpose. It came from ''George F. Simmons'' example in Wikipedia that compares the speed of a car, a bicycle and a walking person. The chain rule applies to differentiate composite functions. Suppose we have a person walking while inside a moving train. If the problem is calculating the person's velocity what we do in physics is to add up vectors because velocity is a vector. Now let's say that the person's velocity is given by a function <math>v_1(t)</math> and the trains' velocity is given by <math>v_2(t)</math>. One could naturally think that because the person is inside the train we have this composition <math>v_2(v_1(t))</math> to describe the person's velocity. This composition doesn't make sense because the function depends on time to calculate a quantity which is space / time. If we have a function that expects the input to be time, inputting space / time is going to produce an error. This reasoning could even lead to someone confusing addition of vectors with products of ratios. <math>[v_2(v_1(t))]' = a_1(t)a_2(v(t))</math> this function is completely wrong in terms of physics. Since when do acceleration depends on velocity? With acceleration being a vector, cross product, dot product and addition are completely different operations with different meanings. Sometimes we try to find a physical interpretation and end up with more confusion than clarity. | |||
==Graphical reasoning for the chain rule== | ==Graphical reasoning for the chain rule== | ||
Revision as of 18:34, 9 April 2022
The chain rule is, intuitively, a product of two derivatives. Suppose we have three moving things: A, B and C and their respective speeds are A > B > C. If we know how many times the speed of A is in comparison to B and B in comparison to C, then we can know how many times A is in comparison to C too. What we have to do is to multiply the ratios between A and B and between B and C. This is the example in Wikipedia's article.
Another example. In meteorology there is the Lapse rate which is the variation in temperature according to how high we are in the atmosphere. To make calculations easier during classes what most teachers do is to use the ratio 10 °C per km. Which means that for every 1 km that we go up in the atmosphere, the temperature should decrease by 10 °C. If we fly up or down we experience changes in temperature because we are moving in respect to each level of temperature in the atmosphere. The other way around doesn't happen because if we stay put the atmosphere won't move up or down in respect to us. Flying faster naturally yields a faster change in temperature. The atmosphere has its own rate temperature / height and we, by flying up or down, also have a rate of change of temperature / height. Doing the product of the two should yield the rate of change of temperature over time.
[math]\displaystyle{ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} }[/math]
The definition of a function states that we have one variable that depends upon another. In the case of composite functions, the value of one function depends on the value of the other function.
[math]\displaystyle{ h'(x) = g'(x) \cdot f'(g(x)) }[/math]
We can have any number of functions nested within another. The rule still holds and the name comes from the fact that we have a chain of operations, a chain of derivatives. I think that the most common mistake with the chain rule is to derive the nested function twice, like this [math]\displaystyle{ g'(x)f'(g'(x)) }[/math]. One way to avoid this common mistake is to remember that we have a product of derivatives, not a composition of derivatives.
Note: sometimes we have composite functions but we don't see them clearly. For example: [math]\displaystyle{ y = \sin^2(x) }[/math]. We can see that we have a product [math]\displaystyle{ y = \sin(x) \sin(x) }[/math], but we could also see it as [math]\displaystyle{ y = x^2 }[/math] and [math]\displaystyle{ x = sin(x) }[/math]. In a more conventional notation: [math]\displaystyle{ f(x) = x^2 }[/math], and [math]\displaystyle{ g(x) = \sin(x) }[/math] and [math]\displaystyle{ f \circ g = \sin^2(x) }[/math]. This is specially common with implicit differentiation.
Wrong reasoning: I'm leaving this here. It's a previous explanation that I had that is confusing and may still serve a purpose. It came from George F. Simmons example in Wikipedia that compares the speed of a car, a bicycle and a walking person. The chain rule applies to differentiate composite functions. Suppose we have a person walking while inside a moving train. If the problem is calculating the person's velocity what we do in physics is to add up vectors because velocity is a vector. Now let's say that the person's velocity is given by a function [math]\displaystyle{ v_1(t) }[/math] and the trains' velocity is given by [math]\displaystyle{ v_2(t) }[/math]. One could naturally think that because the person is inside the train we have this composition [math]\displaystyle{ v_2(v_1(t)) }[/math] to describe the person's velocity. This composition doesn't make sense because the function depends on time to calculate a quantity which is space / time. If we have a function that expects the input to be time, inputting space / time is going to produce an error. This reasoning could even lead to someone confusing addition of vectors with products of ratios. [math]\displaystyle{ [v_2(v_1(t))]' = a_1(t)a_2(v(t)) }[/math] this function is completely wrong in terms of physics. Since when do acceleration depends on velocity? With acceleration being a vector, cross product, dot product and addition are completely different operations with different meanings. Sometimes we try to find a physical interpretation and end up with more confusion than clarity.
Graphical reasoning for the chain rule
I don't know about textbooks that show a graphical interpretation for the chain rule. Let's consider [math]\displaystyle{ f(x) = 3x }[/math] and [math]\displaystyle{ g(x) = x^2 }[/math]. The graph of the former is a straight line and the constant factor is the angular coefficient, greater meaning a stepper inclination. The latter is a parabola. The first has a constant rate of change, the second does not.
The graph of [math]\displaystyle{ g(f(x)) = (3x)^2 }[/math] has a greater rate of change than the graph of [math]\displaystyle{ g(x) = x^2 }[/math]. Think about this: if we choose [math]\displaystyle{ x = 2 }[/math] the rates of change are, at that point and for each function, [math]\displaystyle{ f'(2) = 6 }[/math] and [math]\displaystyle{ g'(2) = 4 }[/math]. For the composite function we have [math]\displaystyle{ g'(f(x)) = f'(2)g'(f(2)) = 6 \cdot 2 \cdot 3 = 36 }[/math]. I did this simple example with positive numbers but the chain rule holds for negative numbers and for more complicated functions.
Note: in this specific case we could have used the product rule. Or even faster, the power rule.
Proof of the chain rule
It's natural to think that the derivative of the composite function is the composition of the derivatives. It's the same intuition that commonly happens with the product and quotient rules. When we have a composition, one function is the dependent variable of the other. We can be easily fooled and think that the derivative of [math]\displaystyle{ f(g(x)) }[/math] is [math]\displaystyle{ f'(g'(x)) }[/math]. Mathematically this doesn't make sense because we just swapped a function by its derivative. Who said that it's right to replace a function by its derivative and expect the result of this operation to be meaningful? Who said that the rate of change of [math]\displaystyle{ f }[/math] depends on the rate of change of [math]\displaystyle{ g }[/math]? Think about this: if a function represents velocity in respect to time, its derivative is acceleration in respect to time. There is no meaning in "derive time in respect to (what)?" In this case time is not even dependent on anything to begin with.
The problem of finding the tangent line describes how a differentiable function can be seen as a linear function if we consider a small enough interval around a point. Let's begin by defining two affine functions:
[math]\displaystyle{ f(x) = ax + b }[/math]
[math]\displaystyle{ g(x) = cx + d }[/math]
Let's take a look at:
[math]\displaystyle{ f(g(x)) = ag(x) + b }[/math]
[math]\displaystyle{ f(cx + d) = a(cx + d) + b }[/math]
[math]\displaystyle{ f \circ g = acx + ad + b }[/math]
Did you notice the product between the angular coefficients, [math]\displaystyle{ a \cdot c }[/math]? If we differentiate the expression [math]\displaystyle{ acx + ad + b }[/math] in respect to [math]\displaystyle{ x }[/math], the operation yields [math]\displaystyle{ ac }[/math]! Surprise! That's not a formal proof though. Let's see what happens if we rewrite the same reasoning with linear approximations in mind: