Parametrization of curves

One may think on the graph of each function for each coordinate and try to find a relationship between the graph of each function and the curve. While it may be possible to do that, it's hard to make the association. With functions we can imagine the graph when the do composition, products and sum of functions. However, doing the same for curves doesn't work well because we'd be trying to make an association between graphs which are plotted with an independent and a dependent variable with a graph that is plotted with two independent variables (each coordinate is linearly independent).

The following idea is pure speculation and I have no idea if it works. In physics laboratories there is the classic free fall experiment where a paper strip is burnt with dots created with a device that produces sparks at a regular interval. By measuring the distance between the dots on the paper we draw some conclusions about the motion of a falling object. Now imagine if an object is moving along some curve in 2D given by some equation with two variables. If we could have paper strips for both axis at the same time and mark them at regular intervals, we could have some information about the rate of change in each axis. I was imagining some apparatus where the object moves and some perpendicular light source, one for each axis, projects spot shadows on each axis at regular intervals. It's easier to think on that with some computer simulation than on a real physical apparatus. The fundamental idea here is about seeing the domain of some motion in realtime. Or better say, the rate of change in each axis in realtime.

References for the physics experiment:

• https://learning.physics.iastate.edu/free-fall-spark-tape
• http://hyperphysics.phy-astr.gsu.edu/hbase/Mechanics/ffallex.html

Converting an equation of two variables into parametric form

The idea is that an equation such as [math]\displaystyle{ 10 = x^2 + y^2 }[/math] can have one variable isolated and expressed as a function of the other. However, if we go straight with algebraic manipulation and write [math]\displaystyle{ x(y) = \ ... }[/math] and [math]\displaystyle{ y(x) = \ ... }[/math] that won't do us much good because we'll end up with two functions with two different variables. What we want to achieve is two functions with the same variable.

The physical concept that is behind parametrization of curves is to decompose a position vector, if we are talking about trajectories, into its coordinates. Take the circular motion for example. We learn in physics that there is a velocity vector that is tangent to the trajectory and another that is perpendicular, pointing towards the center of the circle. That's what we are doing when we have a curve given by some equation and want to find [math]\displaystyle{ x(t) }[/math] and [math]\displaystyle{ y(t) }[/math]. If we are working in 3D space there is also [math]\displaystyle{ z(t) }[/math].

In the graphs below I'm using a cartesian coordinate system, the same that we use to plot functions, to make the vectors' components parallel to the axis and easier to read.

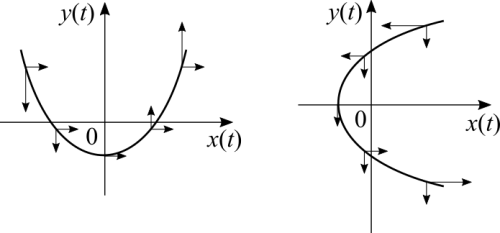
One procedure for obtaining the parametric form of a curve is by using intuition and reasoning based on rates of change. Take a parabola for example. The graph of [math]\displaystyle{ f(x) = x^2 }[/math] can coincide with a trajectory with exactly the same points. Along the horizontal axis we are taking steps at a constant rate of one unit of time. With that in mind we can make an educated guess that we have [math]\displaystyle{ x(t) = t }[/math]. Now the vertical coordinate takes the square of each instant of time, which means [math]\displaystyle{ y(t) = t^2 }[/math]. Those are the two functions that make up the parametric form of a trajectory that is a parabola. Swap the axis and we have a parabola rotated 90° anti-clockwise. Note that the coordinate that has [math]\displaystyle{ t^2 }[/math], the vector's magnitude changes over time. Being equal to zero at the parabola's vertex. The other vector keeps its magnitude unchanged.

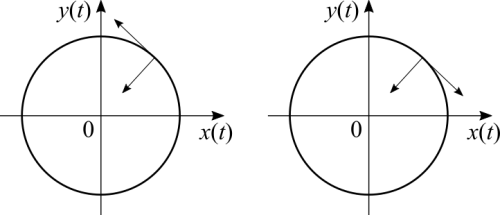
The same idea can be applied for a circle. It has upper and lower bounds. Every X is bounded between [math]\displaystyle{ [-a,\ a] }[/math], the same for Y. What function relates to that? Sine and cosine. Therefore [math]\displaystyle{ (x,\ y) = (\sin(t),\ \cos(t)) }[/math] is a parametric equation that plots a circle on the XY plane. Swapping the order of sine and cosine won't change the circle itself, it'll only change the direction clockwise vs anti-clockwise.

Note: in physics it's very common to make the mistake of placing vectors pointing "outwards" the curve. This is a confusion caused by inertial vs non-inertial frames of reference which I'm not discussing here. In the graph above both of the shown vectors can be decomposed in their respective [math]\displaystyle{ x(t) }[/math] and [math]\displaystyle{ y(t) }[/math] components.

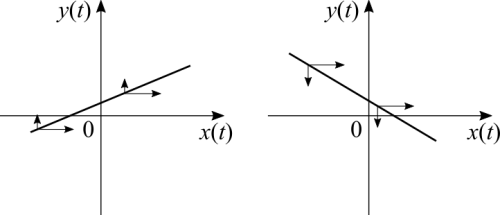
Suppose we have a trajectory that is a straight line. There are multiple parametrizations that result in the same trajectory. The reason for this is because if both coordinates obey to the same function, what is happening to the rate of change, the tangent, rise / run? We have that both coordinates change with the same increments over time. That's a linear behaviour. The difference would be how fast the object is travelling. [math]\displaystyle{ (t^3, \ t^3) }[/math] should have a different velocity compared to [math]\displaystyle{ (t^2, \ t^2) }[/math] but the same trajectory. It's important to keep that in mind, the same trajectory can be travelled at a constant speed, faster or slower over time.

It's important to notice a difference here: if the rate of change in one axis is different from the other axis, that's when we have curves. The magnitude of one component can be different from the other. If the rates of change in both directions are the same, in absolute value, then we have a straight line.

Let's flip from a physical interpretation to a more mathematical one. Take the curve [math]\displaystyle{ xy = 1 }[/math] for example. What we have here is that one variable should be the inverse of the other to keep the equation true. Therefore the parametrization should be [math]\displaystyle{ (t, \ 1/t) }[/math] with [math]\displaystyle{ t \neq 0 }[/math]. We did this: [math]\displaystyle{ t = xy }[/math], then for [math]\displaystyle{ t = 1 }[/math] we conclude that [math]\displaystyle{ y = 1/x }[/math] and [math]\displaystyle{ x = t }[/math]. Our functions are [math]\displaystyle{ x(t) = t }[/math] and [math]\displaystyle{ y(t) = 1/t }[/math].

Going back to the circle, how do we convert polar to cartesian coordinates? With [math]\displaystyle{ x = r\cos \theta }[/math] and [math]\displaystyle{ y = r\sin \theta }[/math]. Take a second look at the formulas, we have that the horizontal and vertical coordinates depend on the same variable, the angle. With the radius being a constant. Let's call [math]\displaystyle{ \theta = t }[/math] and we've just found how to properly parametrize the equation of a circle. Careful! Time now has to be in radians, not just any multiple of seconds. Doesn't the equation of a circle have the same form as the fundamental trigonometric identity? That's another way to see it.