Teoremas sobre limites e continuidade de funções: Difference between revisions
(Created page with "Dependendo do professor e em qual tipo de curso de cálculo esta sendo dado, os teoremas a seguir não são demonstrados em aula porque eles precisam de um nível de abstração que nem todo mundo é familiarizado com. Há ainda a limitação de tempo. Nem sempre é viável fazer as demonstrações. Os teoremas abaixo sempre assumem que as funções são contínuas, porque se não forem contínuas num intervalo não temos como afirmar muitas propriedades. Sempre há doi...") |
No edit summary |
||
| Line 1: | Line 1: | ||
Dependendo do professor e | Dependendo do professor e do tipo de curso de cálculo esta sendo dado, os teoremas a seguir não são demonstrados em aula porque eles precisam de um nível de abstração que nem todo mundo esta familiarizado. Há ainda a limitação de tempo. Nem sempre é viável fazer as demonstrações. | ||
Os teoremas abaixo sempre assumem que as funções são contínuas, porque se não forem contínuas num intervalo não temos como afirmar muitas propriedades. Sempre há dois pontos | Os teoremas abaixo sempre assumem que as funções são contínuas, porque se não forem contínuas num intervalo não temos como afirmar muitas propriedades. Sempre há dois pontos distintos <math>a</math> e <math>b</math>, porque se <math>a = b</math> não temos um intervalo e não podemos afirmar nada sobre a função. Exceto verificar se a função esta definida ali ou não. A distância entre os pontos das extremidades pode ser pequena ou grande, desde que seja positiva. Os gráficos podem diferir de livro para livro e é natural. Estamos tratando de uma pequena parte de uma ideia geral. Não há uma forma de traçar todos os casos um por um, nem traçar no infinito. | ||
'''Antes de prosseguirmos para os teoremas algumas perguntas já podem ser feitas:''' o que fazer se a função tem um ponto onde o limite é infinito? Se este é o caso a função já não é contínua naquele ponto. Portanto, não podemos ter um máximo ali porque o infinito não é um número. Reciprocamente, o infinito negativo não é um mínimo. O que fazer se o limite não existe? Na melhor das hipóteses podemos dizer que a função é limitada entre dois extremos, mas com o limite indefinido não podemos concluir nada sobre um valor que não sabemos ao certo. Você é capaz de saber qual, dentre dois números desconhecidos, é maior? É impossível! Ao assumirmos que as funções são contínuas estamos eliminando casos nos quais o teorema seria inválido. | |||
==Teorema do valor intermediário== | |||
== | |||
<div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | <div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | ||
Se <math>f</math> for contínua em <math>[a, \ b]</math> e <math>f(c)</math> esta entre <math>f(a)</math> e <math>f(b)</math>. Então deverá existir um <math>c</math>, dentro do intervalo, tal que <math>f(c) = c</math>. | |||
[[file:intermediate_value_theorem.png|300px]] | [[file:intermediate_value_theorem.png|300px]] | ||
( | (Este não é o teorema do valor médio) | ||
</div> | </div> | ||
Este teorema pode ser visto como uma extensão do fato de que entre dois números reais sempre há um terceiro. Entre dois valores de uma função sempre há um terceiro. Observe que este teorema só faz sentido partindo do pressuposto que a função é contínua. Não podemos usar deste teorema para provar que uma função é contínua! Este teorema é uma consequência da continuidade da função. A ideia dele é semelhante à do teorema do valor médio. Entre <math>f(a)</math> e <math>f(b)</math> existirá um valor que é a média dos dois anteriores. Acho que é aqui que a confusão entre os dois teoremas acontece. | |||
Um subcaso do teorema do valor intermediário é o '''Teorema de Bolzano'''. Se <math>f(a)f(b) < 0</math>, então a função tem um ponto onde <math>f(x) = 0</math>. Este é um dos primeiros teoremas que aprendemos em aulas de métodos numéricos, porque precisamos dele para achar raízes de equações. Alguém pode pensar em dimensões mais altas. O Teorema de Bolzano só faz sentido no plano cartesiano. Podemos atravessar para o outro lado sem cruzar um eixo ou reta? Em 2D não. Precisamos do espaço 3D para ir ao outro lado sem tocar na linha. Se existe teorema semelhante ao de Bolzano para dimensões maiores não faço ideia. | |||
Podemos comparar aqui o Teorema do Valor Intermediário e a definição formal do limite. O segundo diz que é dado um epsilon e não importa quão pequeno ele seja, sempre haverá um delta correspondente. O primeiro diz que se uma função é contínua entre dois pontos, então a função, necessariamente, assume todos os valores intermediários. Em particular, um destes valores é a média entre os dois extremos do intervalo. | |||
'''Links | '''Links para as demonstrações:''' (em inglês) | ||
* http://mathcenter.oxford.emory.edu/site/math111/proofs/ivt/ | * http://mathcenter.oxford.emory.edu/site/math111/proofs/ivt/ | ||
* https://en.wikipedia.org/wiki/Intermediate_value_theorem | * https://en.wikipedia.org/wiki/Intermediate_value_theorem | ||
| Line 30: | Line 28: | ||
* https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-16/v/intermediate-value-theorem | * https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-16/v/intermediate-value-theorem | ||
==Weierstrass | ==Teorema de Weierstrass ou do valor extremo== | ||
<div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | <div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | ||
Se <math>f</math> for contínua em <math>[a, \ b]</math>. Então existirá <math>x_1</math> e <math>x_2</math>, naquele intervalo, tal que <math>f(x_1) \leq f(x) \leq f(x_2)</math> para todo <math>x</math> em <math>[a, \ b]</math>. | |||
[[file:weierstrass_graph.png|300px]] | [[file:weierstrass_graph.png|300px]] | ||
''( | ''(O teorema não se importa com a função ser constante, crescente ou decrescente no intervalo. Não associe o teorema a um caso específico de função.)'' | ||
</div> | </div> | ||
O que este teorema afirma é: num intervalo fechado a função terá um máximo e um mínimo. O intervalo precisa ser fechado porque se considerarmos um intervalo aberto estaremos aceitando valores para os quais o limite pode ser infinito, o que invalidaria o teorema. Lembre-se que o infinito não faz parte dos números reais. Não podemos calcular uma função no infinito, mas podermos calcular o limite indo para infinito. Ao restringirmos o intervalo para o caso fechado garantimos que a função esta definida e que o limite em todos os seus pontos é finito. | |||
Suponha que temos a função <math>f(x) = 1/x</math>. Se o intervalo for aberto e incluir o zero, nunca iremos dividir por zero. Porém, como o intervalo é aberto podemos chegar infinitamente perto do zero e isto significa aceitar que a função não é limitada porque ela vai para infinito. Se o intervalo for fechado e excluir o zero, quem sabe ele contenha o número 0.0001, que é finito e <math>f(0.0001)</math> é também finito. Qualquer valor entre 0.0001 e 0 não faz parte do intervalo do exemplo. | |||
'''Links | '''Links para as demonstrações:''' (em inglês) | ||
* https://en.wikipedia.org/wiki/Extreme_value_theorem | * https://en.wikipedia.org/wiki/Extreme_value_theorem | ||
* https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-2/v/extreme-value-theorem | * https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-2/v/extreme-value-theorem | ||
| Line 50: | Line 48: | ||
* http://mathcenter.oxford.emory.edu/site/math111/proofs/extremeValueTheorem/ | * http://mathcenter.oxford.emory.edu/site/math111/proofs/extremeValueTheorem/ | ||
==Rolle | ==Teorema de Rolle== | ||
<div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | <div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | ||
Se <math>f</math> for contínua em <math>[a, \ b]</math>, diferenciável em <math>]a, \ b[</math> e <math>f(a) = f(b)</math>. Então existirá um <math>x_1</math>, naquele intervalo, tal que <math>f'(x_1) = 0</math>. | |||
[[file:rolle_graph.png|300px]] | [[file:rolle_graph.png|300px]] | ||
''( | ''(O teorema garante que pelo menos um ponto terá uma derivada igual a zero. Porém, podem haver outros.)'' | ||
</div> | </div> | ||
O que este teorema afirma é que entre dois pontos, de mesma altura, da função, existirá um ponto onde a derivada é zero. Pense sobre isto: se a função é estritamente crescente ou estritamente decrescente, é impossível que ela tenha uma tangente horizontal entre os dois pontos. O teorema diz que se os dois extremos tem o mesmo valor, a função só pode ser constante ou em algum lugar no meio do caminho a taxa de variação inverte de sinal. | |||
O intervalo deve ser fechado pela mesma razão dada no caso do Teorma do Valor Extremo. Por quê o Teorema de Rolle diz que a função é diferenciável num intervalo aberto? Porque há funções com pontos onde o limite existe e é contínua, mas ainda assim não é diferenciável. Por exemplo: <math>f(x) = |x|</math> é diferenciável em todos os seus pontos, exceto pela origem. É por isto que o teorema diz que a função é diferenciável num intervalo aberto. A função pode ser contínua nas extremidades, mas ao mesmo tempo não ser diferenciável naqueles pontos. | |||
'''Links | '''Links para as demonstrações:''' (em inglês) | ||
* https://brilliant.org/wiki/rolles-theorem/ | * https://brilliant.org/wiki/rolles-theorem/ | ||
* http://mathcenter.oxford.emory.edu/site/math111/proofs/rollesTheorem/ | * http://mathcenter.oxford.emory.edu/site/math111/proofs/rollesTheorem/ | ||
| Line 70: | Line 68: | ||
* https://www.cuemath.com/calculus/rolles-theorem/ | * https://www.cuemath.com/calculus/rolles-theorem/ | ||
==Lagrange | ==Teorema do Valor Médio de Lagrange== | ||
<div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | <div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | ||
Se <math>f</math> for contínua em <math>[a, \ b]</math>, diferenciável em <math>]a, \ b[</math>. Então existirá um <math>x_1</math>, naquele intervalo, tal que <math>f'(x_1) = \frac{f(b) - f(a)}{b - a}</math> ou <math>f'(x_1)(b - a) = f(b) - f(a)</math> | |||
[[file:mean_value_graph.png|300px]] | [[file:mean_value_graph.png|300px]] | ||
''( | ''(Este não é o teorema do valor intermediário. O nome é parecido mas é outro teorema. O ponto onde a tangente é paralela À secante não precisa estar entre <math>f(a)</math> e <math>f(b)</math>. É uma confusão que pode acontecer devido à semelhança de ambos os teoremas.)'' | ||
</div> | </div> | ||
O que este teorema afirma é que temos uma secante que passa por dois pontos da função. Entre os dois pontos deve haver uma tangente que é paralela à secante. O teorema não afirma que o ponto da tangente é único, podem haver outros. Partimos do pressuposto que a função é diferenciável, de outra forma a reta tangente pode não existir porque podem haver pontos em que a função é contínua mas não diferenciável. A ideia é bastante parecida com o Teorema de Rolle. De fato, o Teorema de Rolle é um subcaso do Teorema do Valor Médio. | |||
<math>(b - a) \neq 0</math>. | <math>(b - a) \neq 0</math>. Primeiro <math>b \neq a</math>, de outra forma não temos uma taxa de variação. Segundo, quando calculamos o limite da distância conforme esta fica infinitamente pequena. Nunca chegamos a zero de fato. | ||
''' | '''Interpretação física:''' suponha que uma função representa velocidade no tempo. Suponha que num certo intervalo de tempo a velocidade aumenta e diminui. Num dado instante é 20 m/s e em outro é 10 m/s. Aprendemos na escola que a velocidade média é <math>(10 + 20)/2 = 15 \ m/s</math>. O que o teorema diz sobre a velocidade é que deve haver um instante tal que a velocidade é a própria média. Não importa quão rápido a velocidade muda com o tempo. O que importa é que o processo é contínuo. Caso a aceleração seja zero, a velocidade média deverá ser constante em todos os instantes de tempo. | ||
Observe que se tivermos um processo que apresenta uma descontinuidade no intervalo, não poderemos aplicar o teorema. Porque o valor médio pode acontecer justo onde a função é descontínua. | |||
'''Links | '''Links para as demonstrações:''' (em inglês) | ||
* https://en.wikipedia.org/wiki/Mean_value_theorem | * https://en.wikipedia.org/wiki/Mean_value_theorem | ||
* https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-1/v/mean-value-theorem-1 | * https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-1/v/mean-value-theorem-1 | ||
| Line 93: | Line 91: | ||
* https://brilliant.org/wiki/mean-value-theorem/ | * https://brilliant.org/wiki/mean-value-theorem/ | ||
==Cauchy | ==Teorema do Valor Médio de Cauchy== | ||
<div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | <div style="text-align:center; background-color: #f8f9fa; padding:1em;"> | ||
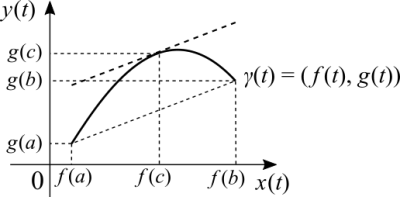
Se <math>f</math> e <math>g</math> são contínuas em <math>[a, \ b]</math>, diferenciáveis em <math>]a, \ b[</math>. Então existirá um <math>c</math> em <math>]a, \ b[</math> tal que <math>[f(b) - f(a)]g'(c) = [g(b) - g(a)]f'(c)</math> | |||
ou | |||
<math>\frac{g(b) - g(a)}{f(b) - f(a)} = \frac{g'(c)}{f'(c)}</math>, | <math>\frac{g(b) - g(a)}{f(b) - f(a)} = \frac{g'(c)}{f'(c)}</math>, se <math>g(a) \neq g(b)</math> e <math>f'(c) \neq 0</math>. | ||
[[file:cauchy_mean_value_graph.png|400px]] | [[file:cauchy_mean_value_graph.png|400px]] | ||
( | (Cuidado com este gráfico! É <math>x(t)</math> x <math>y(t)</math>, não <math>t</math> x <math>\gamma (t)</math>!) | ||
</div> | </div> | ||
Este teorema é uma generalização do Teorema do Valor médio. Suponha que temos duas funções diferentes entre dois pontos e cada uma obedece às condições do Teorema do Valor Médio. Uma pergunta natural surge: se cada função, por si mesma, terá um ponto onde a taxa de variação é igual à taxa de variação média. Então há um ponto onde a taxa de variação de uma função é igual à taxa de variação média da outra? Sim, há. | |||
Cuidado com a interpretação do teorema! Suponha que num ponto <math>x = c</math> temos que a taxa de variação de <math>f</math> é igual à taxa de variação média. Isto não implica que o mesmo ocorra com <math>g</math>! No caso de <math>g</math> o ponto pode estar em outro lugar porque é uma função diferente! O que o teorema afirma é que ambas as funções devem ter a mesma taxa de variação média. Em algum momento na escola aprendemos que dois conjuntos diferentes de números podem ter a mesma média. | |||
Eu tenho um livro que apresenta uma interpretação diferente. Uma curva pode ser uma trajetória, onde cada um dos seus pontos é dado por uma combinação linear de mais de uma função. Temos uma função para cada coordenada. Escolhemos dois pontos e traçamos uma secante. Entre os dois pontos deve haver uma tangente que é paralela à secante. É a mesma ideia geométrica do teorema do valor médio, exceto que uma trajetória é uma função vetorial. Como derivamos uma função vetorial? Derivamos coordenada a coordenada, porque cada uma tem a sua própria função. Em cada ponto da curva temos o mesmo parâmetro, que no caso das trajetórias é o tempo. | |||
'''Links | '''Links para as demonstrações:''' | ||
* https://en.wikipedia.org/wiki/Mean_value_theorem#Cauchy's_mean_value_theorem | * https://en.wikipedia.org/wiki/Mean_value_theorem#Cauchy's_mean_value_theorem | ||
* https://math24.net/cauchys-mean-value-theorem.html | * https://math24.net/cauchys-mean-value-theorem.html | ||
* https://proofwiki.org/wiki/Cauchy_Mean_Value_Theorem | * https://proofwiki.org/wiki/Cauchy_Mean_Value_Theorem | ||
Revision as of 01:02, 14 August 2022
Dependendo do professor e do tipo de curso de cálculo esta sendo dado, os teoremas a seguir não são demonstrados em aula porque eles precisam de um nível de abstração que nem todo mundo esta familiarizado. Há ainda a limitação de tempo. Nem sempre é viável fazer as demonstrações.
Os teoremas abaixo sempre assumem que as funções são contínuas, porque se não forem contínuas num intervalo não temos como afirmar muitas propriedades. Sempre há dois pontos distintos [math]\displaystyle{ a }[/math] e [math]\displaystyle{ b }[/math], porque se [math]\displaystyle{ a = b }[/math] não temos um intervalo e não podemos afirmar nada sobre a função. Exceto verificar se a função esta definida ali ou não. A distância entre os pontos das extremidades pode ser pequena ou grande, desde que seja positiva. Os gráficos podem diferir de livro para livro e é natural. Estamos tratando de uma pequena parte de uma ideia geral. Não há uma forma de traçar todos os casos um por um, nem traçar no infinito.
Antes de prosseguirmos para os teoremas algumas perguntas já podem ser feitas: o que fazer se a função tem um ponto onde o limite é infinito? Se este é o caso a função já não é contínua naquele ponto. Portanto, não podemos ter um máximo ali porque o infinito não é um número. Reciprocamente, o infinito negativo não é um mínimo. O que fazer se o limite não existe? Na melhor das hipóteses podemos dizer que a função é limitada entre dois extremos, mas com o limite indefinido não podemos concluir nada sobre um valor que não sabemos ao certo. Você é capaz de saber qual, dentre dois números desconhecidos, é maior? É impossível! Ao assumirmos que as funções são contínuas estamos eliminando casos nos quais o teorema seria inválido.
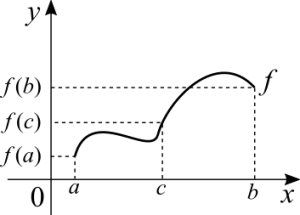
Teorema do valor intermediário
Se [math]\displaystyle{ f }[/math] for contínua em [math]\displaystyle{ [a, \ b] }[/math] e [math]\displaystyle{ f(c) }[/math] esta entre [math]\displaystyle{ f(a) }[/math] e [math]\displaystyle{ f(b) }[/math]. Então deverá existir um [math]\displaystyle{ c }[/math], dentro do intervalo, tal que [math]\displaystyle{ f(c) = c }[/math].
(Este não é o teorema do valor médio)
Este teorema pode ser visto como uma extensão do fato de que entre dois números reais sempre há um terceiro. Entre dois valores de uma função sempre há um terceiro. Observe que este teorema só faz sentido partindo do pressuposto que a função é contínua. Não podemos usar deste teorema para provar que uma função é contínua! Este teorema é uma consequência da continuidade da função. A ideia dele é semelhante à do teorema do valor médio. Entre [math]\displaystyle{ f(a) }[/math] e [math]\displaystyle{ f(b) }[/math] existirá um valor que é a média dos dois anteriores. Acho que é aqui que a confusão entre os dois teoremas acontece.
Um subcaso do teorema do valor intermediário é o Teorema de Bolzano. Se [math]\displaystyle{ f(a)f(b) \lt 0 }[/math], então a função tem um ponto onde [math]\displaystyle{ f(x) = 0 }[/math]. Este é um dos primeiros teoremas que aprendemos em aulas de métodos numéricos, porque precisamos dele para achar raízes de equações. Alguém pode pensar em dimensões mais altas. O Teorema de Bolzano só faz sentido no plano cartesiano. Podemos atravessar para o outro lado sem cruzar um eixo ou reta? Em 2D não. Precisamos do espaço 3D para ir ao outro lado sem tocar na linha. Se existe teorema semelhante ao de Bolzano para dimensões maiores não faço ideia.
Podemos comparar aqui o Teorema do Valor Intermediário e a definição formal do limite. O segundo diz que é dado um epsilon e não importa quão pequeno ele seja, sempre haverá um delta correspondente. O primeiro diz que se uma função é contínua entre dois pontos, então a função, necessariamente, assume todos os valores intermediários. Em particular, um destes valores é a média entre os dois extremos do intervalo.
Links para as demonstrações: (em inglês)
- http://mathcenter.oxford.emory.edu/site/math111/proofs/ivt/
- https://en.wikipedia.org/wiki/Intermediate_value_theorem
- https://brilliant.org/wiki/intermediate-value-theorem/
- https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-16/v/intermediate-value-theorem
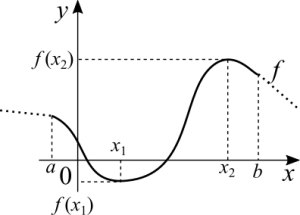
Teorema de Weierstrass ou do valor extremo
Se [math]\displaystyle{ f }[/math] for contínua em [math]\displaystyle{ [a, \ b] }[/math]. Então existirá [math]\displaystyle{ x_1 }[/math] e [math]\displaystyle{ x_2 }[/math], naquele intervalo, tal que [math]\displaystyle{ f(x_1) \leq f(x) \leq f(x_2) }[/math] para todo [math]\displaystyle{ x }[/math] em [math]\displaystyle{ [a, \ b] }[/math].
(O teorema não se importa com a função ser constante, crescente ou decrescente no intervalo. Não associe o teorema a um caso específico de função.)
O que este teorema afirma é: num intervalo fechado a função terá um máximo e um mínimo. O intervalo precisa ser fechado porque se considerarmos um intervalo aberto estaremos aceitando valores para os quais o limite pode ser infinito, o que invalidaria o teorema. Lembre-se que o infinito não faz parte dos números reais. Não podemos calcular uma função no infinito, mas podermos calcular o limite indo para infinito. Ao restringirmos o intervalo para o caso fechado garantimos que a função esta definida e que o limite em todos os seus pontos é finito.
Suponha que temos a função [math]\displaystyle{ f(x) = 1/x }[/math]. Se o intervalo for aberto e incluir o zero, nunca iremos dividir por zero. Porém, como o intervalo é aberto podemos chegar infinitamente perto do zero e isto significa aceitar que a função não é limitada porque ela vai para infinito. Se o intervalo for fechado e excluir o zero, quem sabe ele contenha o número 0.0001, que é finito e [math]\displaystyle{ f(0.0001) }[/math] é também finito. Qualquer valor entre 0.0001 e 0 não faz parte do intervalo do exemplo.
Links para as demonstrações: (em inglês)
- https://en.wikipedia.org/wiki/Extreme_value_theorem
- https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-2/v/extreme-value-theorem
- https://www.opentextbooks.org.hk/ditatopic/34200
- http://mathcenter.oxford.emory.edu/site/math111/proofs/extremeValueTheorem/
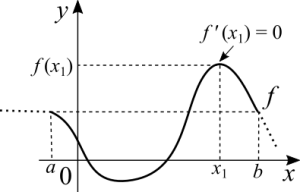
Teorema de Rolle
Se [math]\displaystyle{ f }[/math] for contínua em [math]\displaystyle{ [a, \ b] }[/math], diferenciável em [math]\displaystyle{ ]a, \ b[ }[/math] e [math]\displaystyle{ f(a) = f(b) }[/math]. Então existirá um [math]\displaystyle{ x_1 }[/math], naquele intervalo, tal que [math]\displaystyle{ f'(x_1) = 0 }[/math].
(O teorema garante que pelo menos um ponto terá uma derivada igual a zero. Porém, podem haver outros.)
O que este teorema afirma é que entre dois pontos, de mesma altura, da função, existirá um ponto onde a derivada é zero. Pense sobre isto: se a função é estritamente crescente ou estritamente decrescente, é impossível que ela tenha uma tangente horizontal entre os dois pontos. O teorema diz que se os dois extremos tem o mesmo valor, a função só pode ser constante ou em algum lugar no meio do caminho a taxa de variação inverte de sinal.
O intervalo deve ser fechado pela mesma razão dada no caso do Teorma do Valor Extremo. Por quê o Teorema de Rolle diz que a função é diferenciável num intervalo aberto? Porque há funções com pontos onde o limite existe e é contínua, mas ainda assim não é diferenciável. Por exemplo: [math]\displaystyle{ f(x) = |x| }[/math] é diferenciável em todos os seus pontos, exceto pela origem. É por isto que o teorema diz que a função é diferenciável num intervalo aberto. A função pode ser contínua nas extremidades, mas ao mesmo tempo não ser diferenciável naqueles pontos.
Links para as demonstrações: (em inglês)
- https://brilliant.org/wiki/rolles-theorem/
- http://mathcenter.oxford.emory.edu/site/math111/proofs/rollesTheorem/
- https://en.wikipedia.org/wiki/Rolle%27s_theorem
- https://www.cuemath.com/calculus/rolles-theorem/
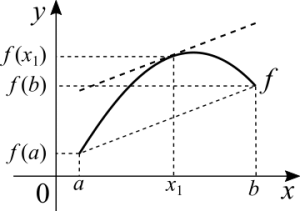
Teorema do Valor Médio de Lagrange
Se [math]\displaystyle{ f }[/math] for contínua em [math]\displaystyle{ [a, \ b] }[/math], diferenciável em [math]\displaystyle{ ]a, \ b[ }[/math]. Então existirá um [math]\displaystyle{ x_1 }[/math], naquele intervalo, tal que [math]\displaystyle{ f'(x_1) = \frac{f(b) - f(a)}{b - a} }[/math] ou [math]\displaystyle{ f'(x_1)(b - a) = f(b) - f(a) }[/math]
(Este não é o teorema do valor intermediário. O nome é parecido mas é outro teorema. O ponto onde a tangente é paralela À secante não precisa estar entre [math]\displaystyle{ f(a) }[/math] e [math]\displaystyle{ f(b) }[/math]. É uma confusão que pode acontecer devido à semelhança de ambos os teoremas.)
O que este teorema afirma é que temos uma secante que passa por dois pontos da função. Entre os dois pontos deve haver uma tangente que é paralela à secante. O teorema não afirma que o ponto da tangente é único, podem haver outros. Partimos do pressuposto que a função é diferenciável, de outra forma a reta tangente pode não existir porque podem haver pontos em que a função é contínua mas não diferenciável. A ideia é bastante parecida com o Teorema de Rolle. De fato, o Teorema de Rolle é um subcaso do Teorema do Valor Médio.
[math]\displaystyle{ (b - a) \neq 0 }[/math]. Primeiro [math]\displaystyle{ b \neq a }[/math], de outra forma não temos uma taxa de variação. Segundo, quando calculamos o limite da distância conforme esta fica infinitamente pequena. Nunca chegamos a zero de fato.
Interpretação física: suponha que uma função representa velocidade no tempo. Suponha que num certo intervalo de tempo a velocidade aumenta e diminui. Num dado instante é 20 m/s e em outro é 10 m/s. Aprendemos na escola que a velocidade média é [math]\displaystyle{ (10 + 20)/2 = 15 \ m/s }[/math]. O que o teorema diz sobre a velocidade é que deve haver um instante tal que a velocidade é a própria média. Não importa quão rápido a velocidade muda com o tempo. O que importa é que o processo é contínuo. Caso a aceleração seja zero, a velocidade média deverá ser constante em todos os instantes de tempo.
Observe que se tivermos um processo que apresenta uma descontinuidade no intervalo, não poderemos aplicar o teorema. Porque o valor médio pode acontecer justo onde a função é descontínua.
Links para as demonstrações: (em inglês)
- https://en.wikipedia.org/wiki/Mean_value_theorem
- https://www.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-1/v/mean-value-theorem-1
- http://mathcenter.oxford.emory.edu/site/math111/proofs/meanValueTheorem/
- https://brilliant.org/wiki/mean-value-theorem/
Teorema do Valor Médio de Cauchy
Se [math]\displaystyle{ f }[/math] e [math]\displaystyle{ g }[/math] são contínuas em [math]\displaystyle{ [a, \ b] }[/math], diferenciáveis em [math]\displaystyle{ ]a, \ b[ }[/math]. Então existirá um [math]\displaystyle{ c }[/math] em [math]\displaystyle{ ]a, \ b[ }[/math] tal que [math]\displaystyle{ [f(b) - f(a)]g'(c) = [g(b) - g(a)]f'(c) }[/math]
ou
[math]\displaystyle{ \frac{g(b) - g(a)}{f(b) - f(a)} = \frac{g'(c)}{f'(c)} }[/math], se [math]\displaystyle{ g(a) \neq g(b) }[/math] e [math]\displaystyle{ f'(c) \neq 0 }[/math].
(Cuidado com este gráfico! É [math]\displaystyle{ x(t) }[/math] x [math]\displaystyle{ y(t) }[/math], não [math]\displaystyle{ t }[/math] x [math]\displaystyle{ \gamma (t) }[/math]!)
Este teorema é uma generalização do Teorema do Valor médio. Suponha que temos duas funções diferentes entre dois pontos e cada uma obedece às condições do Teorema do Valor Médio. Uma pergunta natural surge: se cada função, por si mesma, terá um ponto onde a taxa de variação é igual à taxa de variação média. Então há um ponto onde a taxa de variação de uma função é igual à taxa de variação média da outra? Sim, há.
Cuidado com a interpretação do teorema! Suponha que num ponto [math]\displaystyle{ x = c }[/math] temos que a taxa de variação de [math]\displaystyle{ f }[/math] é igual à taxa de variação média. Isto não implica que o mesmo ocorra com [math]\displaystyle{ g }[/math]! No caso de [math]\displaystyle{ g }[/math] o ponto pode estar em outro lugar porque é uma função diferente! O que o teorema afirma é que ambas as funções devem ter a mesma taxa de variação média. Em algum momento na escola aprendemos que dois conjuntos diferentes de números podem ter a mesma média.
Eu tenho um livro que apresenta uma interpretação diferente. Uma curva pode ser uma trajetória, onde cada um dos seus pontos é dado por uma combinação linear de mais de uma função. Temos uma função para cada coordenada. Escolhemos dois pontos e traçamos uma secante. Entre os dois pontos deve haver uma tangente que é paralela à secante. É a mesma ideia geométrica do teorema do valor médio, exceto que uma trajetória é uma função vetorial. Como derivamos uma função vetorial? Derivamos coordenada a coordenada, porque cada uma tem a sua própria função. Em cada ponto da curva temos o mesmo parâmetro, que no caso das trajetórias é o tempo.
Links para as demonstrações: