Definindo a derivada

Antes da discussão eu devo esclarecer uma confusão que aconteceu comigo. Todo livro discute o problema de achar a reta tangente antes de definir a derivada de uma função. Se você já assistiu um vídeo a respeito, quem sabe o clipe "I will derive", você deve ter testemunhado a reta tangente deslizando sobre gráfico da função como se fosse uma montanha-russa. Cuidado aí! A reta tangente é uma coisa. A derivada de uma função não é a própria reta tangente! Quando calculamos um limite ele produz dois possíveis resultados: um número ou infinito. A definição da derivada é um limite, mas neste caso o resultado é uma outra função. Pode acontecer da derivada resultar num número, que no caso é uma função constante.

Eu menciono esta confusão porque eu acredito que é muito comum as pessoas se enganarem, pensando que derivar uma função é a mesma coisa que achar a reta tangente. Não exatamente. Quando temos funções como polinomiais de um grau maior do que 2 e qualquer função transcendental, o processo de calcular uma derivada produz uma outra função que não é linear. Não é uma linha reta! Não existe o problema de achar uma função que seja tangente a outra em múltiplos pontos.

O problema da reta tangente

         

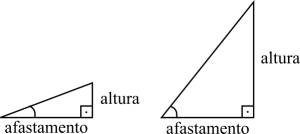
A definição da tangente é a razão altura / afastamento num triângulo retângulo. Na escola os comprimentos dos lados de um triângulo são dados ou nós medimos com uma régua. Com a geometria analítica sabemos que a distância entre dois pontos, tais que o segmento seja paralelo ao eixo, é [math]\displaystyle{ |a - b| }[/math]. Quando a altura é próxima do zero o ângulo é próximo do zero. Isso significa que a rampa tem uma inclinação muito pequena. O oposto é quando a altura é tão exageradamente grande que o ângulo se aproxima de 90°, a maior inclinação possível.

    [math]\displaystyle{ \text{tan} = \frac{f(x) - f(p)}{x - p} }[/math]

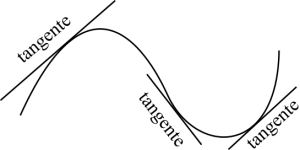
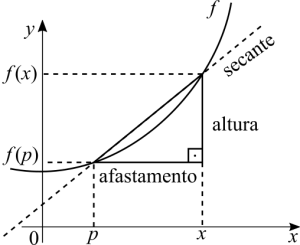
Cuidado aqui! A hipotenusa do triângulo não é a tangente. É uma secante porque esta cruzando o gráfico em dois pontos. Para a fazer a reta secante se tornar uma tangente precisamos de um limite e fazer a distância entre os dois pontos muito pequena.

[math]\displaystyle{ \lim_{x \ \to \ p} \frac{f(x) - f(p)}{x - p} }[/math]

O que o limite esta calculando é a inclinação daquele ponto. Se pudéssemos desenhar um triângulo retângulo numa escala microscópica, teríamos a razão altura / afastamento igual àquele número.

Nota de rodapé: sobre a ordem dos pontos. Dependendo do livro a concavidade do gráfico esta para cima ou para baixo. É por isso que a ordem dos pontos no limite acima esta trocada em relação ao padrão, que seria o [math]\displaystyle{ p }[/math] à direita de [math]\displaystyle{ x }[/math]. Como a notação padrão é [math]\displaystyle{ f(x) }[/math] é mais natural escrever [math]\displaystyle{ x \to p }[/math] do que ao contrário.

A derivada

Podemos escrever o mesmo limite acima com uma notação ligeiramente diferente. A nova notação enfatiza a ideia do limite mais do que a ideia geométrica da razão altura / afastamento. [math]\displaystyle{ \text{afastamento} = |x - p| }[/math] and [math]\displaystyle{ \text{altura} = |f(x) - f(p)| }[/math]. Vamos chamar o afastamento de [math]\displaystyle{ h }[/math]. [math]\displaystyle{ x \gt p }[/math] e [math]\displaystyle{ f(x) \gt f(p) }[/math] de acordo com a figura acima. Chamando o afastamento de [math]\displaystyle{ h }[/math], podemos escrever [math]\displaystyle{ f(x) = f(p + h) }[/math].

[math]\displaystyle{ f'(p) = \lim_{h \ \to \ 0} \frac{f(p + h) - f(p)}{h} }[/math]

A interpretação é a de que estamos diminuindo a distância entre [math]\displaystyle{ x }[/math] e [math]\displaystyle{ p }[/math] infinitamente, mas sem chegar no zero. Isto é importante. Quando resolvemos exercícios com esta definição podemos fazer isto [math]\displaystyle{ h/h = 1 }[/math] porque não estamos dividindo por zero.

Em alguns lugares o [math]\displaystyle{ h }[/math] é trocado por [math]\displaystyle{ \Delta x }[/math] ou [math]\displaystyle{ \Delta h }[/math]. A letra Delta em física é associada com mudança ou diferença, como no caso da velocidade média onde escrevemos [math]\displaystyle{ \Delta S_2 - \Delta S_1 = \Delta S }[/math]. É uma outra forma de expressar a ideia de incrementos, de um ponto até o próximo.

Nota de rodapé: O que aconteceu com [math]\displaystyle{ x }[/math] no limite acima? Eu acabei usando [math]\displaystyle{ p }[/math] apenas porque eu estava me referindo à figura acima e não quis repetir o mesmo gráfico.

Notação de Leibniz: [math]\displaystyle{ \frac{dy}{dx} }[/math]. É parecido com uma razão, mas o seu significado não é uma razão. Se olharmos para o problema de achar a reta tangente, a tangente é uma razão associada à dois pontos. Temos [math]\displaystyle{ a }[/math] e [math]\displaystyle{ b }[/math] e [math]\displaystyle{ f(a) }[/math] e [math]\displaystyle{ f(b) }[/math]. Nós usamos destes pontos para traçar um triângulo e visualizar a taxa de variação como uma razão, porque ela realmente é uma razão. Na física é comum associar [math]\displaystyle{ \Delta S/\Delta t }[/math] com a velocidade, porque é uma razão entre a variação do espaço pela variação do tempo. É bastante intuitivo associar a derivada com a tangente e uma razão. Séculos atrás, quando Leibniz estava desenvolvendo o cálculo, ele provavelmente tinha esta interpretação geométrica.

Já no caso de [math]\displaystyle{ \frac{df}{dx} = \frac{d}{dx}f(x) }[/math] temos um problema relacionado ao significado do infinitésimo e não aprendemos isto em cálculo. A menos que o professor tome tempo para explicar, porque é preciso conhecimento de conceitos mais avançados do que os vistos em cálculo pela primeira vez. Por quê podemos dividir por [math]\displaystyle{ dx }[/math]? Porque ele representa "infinitamente próximo do zero". Agora uma função propriamente não é um número, [math]\displaystyle{ df }[/math] representa a variação de [math]\displaystyle{ f(a) }[/math] até [math]\displaystyle{ f(b) }[/math] quando [math]\displaystyle{ a \neq b }[/math]. O grande problema por trás da palavra "infinitésimo" é que ela tenta passar a ideia do menor número possível, que não existe porque se escrevermos um, sempre haverá um menor ainda. Pela mesma razão, o maior número possível não pode ser escrito porque se o fizermos sempre poderemos somar um.

Eu disse "dividir" e que [math]\displaystyle{ \frac{dy}{dx} }[/math] não é uma razão. Vamos clarificar:

[math]\displaystyle{ \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} }[/math] (Na verdade, Leibniz realmente usou a mesma notação de uma divisão porque o limite tem um quociente. Porém, estamos lidando com um limite e com limites temos o caso especial de dividir por algo muito próximo do zero sem chegar no zero propriamente)

Quando temos uma derivada e queremos calcular o seu valor em [math]\displaystyle{ x = a }[/math] é normal associá-la com o problema da reta tangente e a razão altura / afastamento. O problema acontece quando interpretamos a derivada como uma função. Uma função tem dois conjuntos, o domínio e o contradomínio e é aí que a ideia de uma razão entre dois conjuntos de números perde o sentido.

Para derivadas de segunda ordem escrevemos [math]\displaystyle{ \frac{d^2y}{dx^2} = \frac{dy}{dx}\left(\frac{dy}{dx}\right) }[/math]. Esta notação é bastante confusa num primeiro momento porque não estamos elevando ao quadrado. Não é uma potência. O parentesis não significa que estamos calculando um produto. Ele significa que temos uma derivada e estamos calculando a derivada segunda, a derivada da derivada. Esta notação é mais comum com funções de várias variáveis do que com funções de uma variável só.

Notação de Lagrange: [math]\displaystyle{ f'(x) }[/math]. Esta notação tem a vantagem de deixar claro que a derivada é realmente uma função. Leia-se "f linha". Se a linha é uma referência à tangente em si não sei dizer. Derive de novo e temos [math]\displaystyle{ f''(x) }[/math] (f duas linhas) e podemos continuar indefinidamente.

Esta notação [math]\displaystyle{ \frac{dy}{dx} \Bigg|_{x \ = \ 1} }[/math] tem o mesmo significado de [math]\displaystyle{ f'(1) }[/math].

Notação de Newton: [math]\displaystyle{ \dot{x} }[/math], [math]\displaystyle{ \ddot{x} }[/math] e assim por diante. Eu não faço ideia da origem desta notação criada por Newton, mas ela é comum na mecânica e em alguns ramos da física.

Operador diferencial: [math]\displaystyle{ Df }[/math] é chamado de operador diferencial. Um operador diferencial de segunda ordem é [math]\displaystyle{ D^2f }[/math]. Quando calculamos uma derivada, o processo de achar a derivada é chamado de diferenciação. Eu não sei análise funcional, mas a palavra "operador" é semelhante ás operações aritméticas básicas que todos sabemos. Adicionamos um número a outro para obtermos um terceiro. Operamos com funções para produzir outras funções.