Examples of domain of a multivariable function: Difference between revisions
From Applied Science
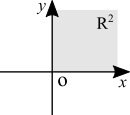
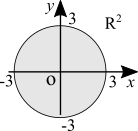
(Created page with "{| class="wikitable" |- | style="padding: 1em; text-align: center;" | file:dom_ex0.png || style="padding: 1em;"| <math>f(x,y) = xy</math>. Both <math>x</math> and <math>y</math> can assume any real value. Therefore the domain is <math>\mathbb{R}^2</math>. |- | style="padding: 1em; text-align: center;" | file:dom_ex1.png || style="padding: 1em;"| <math>f(x,y) = \sqrt{x} + \sqrt{y}</math>. It's analogous to a single variable. Domain is <math>\{(x, \ y) \in \mathbb{...") |
No edit summary |
||
| Line 12: | Line 12: | ||
|- | |- | ||
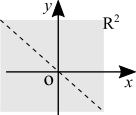
| style="padding: 1em; text-align: center;" | [[file:dom_ex5.png]] || style="padding: 1em;"| <math>f(x,y) = 1/(x + y)</math>. This is easy. To avoid the division by zero we want all pairs where <math>x \neq -y</math> and <math>-x \neq y</math>. In other words, every pair which doesn't obey <math>f(x) = -x</math>. Domain is <math>\{(x, \ y) \in \mathbb{R}^2 : x \neq -y \ \ \text{and} \ -x \neq y\}</math> | | style="padding: 1em; text-align: center;" | [[file:dom_ex5.png]] || style="padding: 1em;"| <math>f(x,y) = 1/(x + y)</math>. This is easy. To avoid the division by zero we want all pairs where <math>x \neq -y</math> and <math>-x \neq y</math>. In other words, every pair which doesn't obey <math>f(x) = -x</math>. Domain is <math>\{(x, \ y) \in \mathbb{R}^2 : x \neq -y \ \ \text{and} \ -x \neq y\}</math> | ||
|} | |||
==Domain of functions of three variables== | |||
{| class="wikitable" | |||
|- | |||
| style="padding: 1em;" | <math>f(x,y,z) = \sqrt{1 - x^2 - y^2 - z^2}</math> || style="padding: 1em;" | The domain is <math>x^2 + y^2 + z^2 \geq 1</math>. We have a sphere of radius 1 and the domain is all points outside the sphere, including its surface. Points inside the sphere result in a complex number. | |||
|- | |||
| style="padding: 1em;" | <math>f(x,y,z) = \sqrt{1 - z}</math> || style="padding: 1em;" | The domain is all <math>z \leq 1</math> because any <math>z > 1</math> results in a complex number. The other two variables are free, which means that the domain is all the space under the plane <math>z = 1</math>, including the plane itself. | |||
|- | |||
| style="padding: 1em;" | <math>f(x,y,z) = \sqrt{1 - x - y - z}</math> <br />for all <math>x \geq 0, y \geq 0, z \geq 0</math>|| style="padding: 1em;" | For the condition given we know that this function's domain is limited between 1 and 0 in all directions. The domain is a prism with some edges equal to 1 and other edges equal to <math>\sqrt{2}</math>. It's hard to picture it, but the square root cannot be negative. The lowest number is zero. The sum of the three variables can't be greater than 1, making 1 the upper bound. | |||
|- | |||
| style="padding: 1em;" | <math>f(x,y,z) = \sqrt{1 - |x| - |y| - |z|}</math> || style="padding: 1em;" | This is slightly more complicated than the previous. Disregard two variables, the remaining variable can be anything between 1 and -1. With this reasoning the variables are all limited between 1 and -1. Now on the XY plane, if we connect <math>(0,1)</math> to <math>(1,0)</math> we have a triangle. Repeat for the XZ and YZ planes and we have more triangles. Repeat for negative coordinates. The domain of this function resembles an icosahedron. It's hard to plot it without a computer. | |||
|} | |} | ||
Latest revision as of 01:15, 22 January 2022
Domain of functions of three variables
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - x^2 - y^2 - z^2} }[/math] | The domain is [math]\displaystyle{ x^2 + y^2 + z^2 \geq 1 }[/math]. We have a sphere of radius 1 and the domain is all points outside the sphere, including its surface. Points inside the sphere result in a complex number. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - z} }[/math] | The domain is all [math]\displaystyle{ z \leq 1 }[/math] because any [math]\displaystyle{ z \gt 1 }[/math] results in a complex number. The other two variables are free, which means that the domain is all the space under the plane [math]\displaystyle{ z = 1 }[/math], including the plane itself. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - x - y - z} }[/math] for all [math]\displaystyle{ x \geq 0, y \geq 0, z \geq 0 }[/math] |
For the condition given we know that this function's domain is limited between 1 and 0 in all directions. The domain is a prism with some edges equal to 1 and other edges equal to [math]\displaystyle{ \sqrt{2} }[/math]. It's hard to picture it, but the square root cannot be negative. The lowest number is zero. The sum of the three variables can't be greater than 1, making 1 the upper bound. |
| [math]\displaystyle{ f(x,y,z) = \sqrt{1 - |x| - |y| - |z|} }[/math] | This is slightly more complicated than the previous. Disregard two variables, the remaining variable can be anything between 1 and -1. With this reasoning the variables are all limited between 1 and -1. Now on the XY plane, if we connect [math]\displaystyle{ (0,1) }[/math] to [math]\displaystyle{ (1,0) }[/math] we have a triangle. Repeat for the XZ and YZ planes and we have more triangles. Repeat for negative coordinates. The domain of this function resembles an icosahedron. It's hard to plot it without a computer. |