Visualising the domain of a function

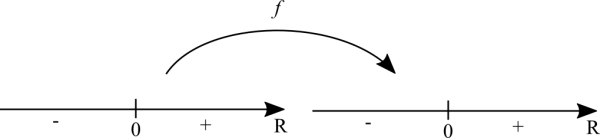
For functions of one variable the domain of a function is quite easy to plot. It's a number line. The function takes elements from the number line, processes them and produces another number line. For most of the time in a calculus course we are concerned with the real numbers. Complex numbers are usually left to a later stage.

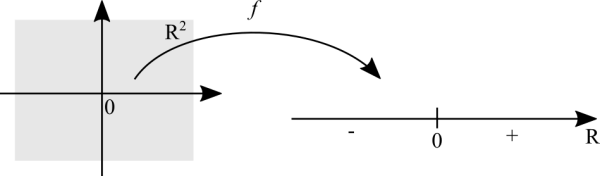
For two variables we are considering the whole Cartesian plane and all pairs (x,y) in it. For three variables it's all points (x,y,z) from the 3D space and then it's not practical to plot by hand. For four or more variables it's the hyperspace, impossible to view.

The domain of a function of two variables can resemble the graph of a function of one variable. However, graphs of single variable functions are always 1D, in the sense that they are lines with zero thickness. A single variable function can never plot any 2D shape with an area. By analogy, the domain of a function of three variables is contained in the 3D space. Functions of two variables can plot sheets, surfaces, planes, but never all points inside a sphere, cube or a cone for example.

A simple way to imagine the domain of a function of one or two variables is to picture a shadow. Under one specific condition, the imaginary light source is perpendicular to the XY plane and all light rays are parallel to each other. What's the shadow of a cable? A thin line. What's the shadow of half a spherical dome? A circle. Careful, we are considering the projected shadow over a flat surface, not the whole space that is obscured by the cable or the dome. Notice that if we stretch or squeeze the graph vertically, the shadow keeps the same shape. The shadow also disregards any irregularities or oscillations in between the extreme points or edges. That same idea can be extended to higher dimensions. A 4D object projects a 3D shadow for example.

In the computer graphics world the idea of projected shadows is the basic concept behind rendering lights and shadows. We evaluate which points are being hit by a light ray and which ones aren't. Under the simplest model, either a surface allows light to pass or not.