Sine, cosine and tangent

At school we first learn how to measure angles and how to add and subtract angles. Later on comes the idea of sine, cosine and tangent. There is a question that is left unanswered until we learn the definitions of sine, cosine and tangent. The question is: we know that a ramp can be harder to walk on according to how much inclined it is, with flat being zero angle and 90° the hardest. Is there a relationship of how many units we walk forwards and how many units we go up if we are walking over a ramp with an angle greater than zero? This is exactly what sine, cosine and tangent are. Ratios that relate angles to sides of a triangle such that we have the answer for the previous mentioned question.

Note: angles do not make sense if we do not have at least two dimensions.

Caution: we always define tangent, cosine and sine with a right triangle. If the triangle does not have a right angle we cannot state that the proportions hold. In fact, they don't.

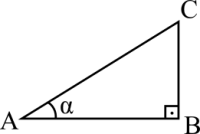AB = run = base BC = rise = height AC = ramp = hypotenuse

In Euclidean geometry the sum of all internal angles must be equal to 180°. With the right triangle having one angle being 90°, the sum of the other two must be 90°. This explains why we never have to memorize rules or properties beyond 90°, because we don't need to.

[math]\displaystyle{ \sin(\alpha) = \frac{BC}{AC} }[/math]. It means how many units we are going up in respect to how many units we are walking forwards over the ramp. What happens if the angle is zero? Then we are not going up no matter how many units we go forwards. This explains [math]\displaystyle{ \sin(0^{\text{o}}) = 0 }[/math]. What happens if the angle is 90°? Then we have a 1:1 ratio, for each unit of the triangle's height we walk over the ramp by the same units. This explains [math]\displaystyle{ \sin(90^{\text{o}}) = 1 }[/math].

[math]\displaystyle{ \cos(\alpha) = \frac{AB}{AC} }[/math]. It means how many units we are going forwards in respect to how many units we are walking up over the ramp. What happens if the angle is zero? Then we have a 1:1 ratio, for each unit of the triangle's run we walk over the ramp by the same units. This explains [math]\displaystyle{ \cos(0^{\text{o}}) = 1 }[/math]. What happens if the angle is 90°? Then we are not moving forwards while going up. This explains [math]\displaystyle{ \cos(90^{\text{o}}) = 0 }[/math].

[math]\displaystyle{ \tan(\alpha) = \frac{BC}{AB} }[/math]. It means how many units we are going up in respect to how many units we are going forwards. What happens if the angle is 90°? The tangent doesn't exist. Think about a circle on the plane and a point in its perimeter, a perpendicular line (on the same plane) cannot be tangent to that point, it's impossible. What happens if the angle is 45°? Then we have a 1:1 ratio, for each unit we go forwards we also go up by the same unit. This explains [math]\displaystyle{ \tan(45^{\text{o}}) = 1 }[/math]. What happens if the angle is zero? Then we are not going up for each unit we walk forwards. It's the same as being parallel.

It's pretty easy to confuse sine with cosine and, for the same reason, invert the two and confuse the tangent too. At school there are some puns that people make to memorize that the horizontal axis is x and the vertical is y. If you look at the triangle above, sine of the angle is always the opposite side divided by the ramp's length. Cosine being the adjacent side divided by the ramp's length. Tangent being height / base. I think this is a way to memorize that sine is always related to the height first, whereas cosine is the base first. Therefore, the vertical / horizontal ratio is the tangent.

There are numerous practical examples that teachers use to demonstrate trigonometry in the real world: length of shadows, height of buildings, solar clocks, etc. Physics has many examples such as stone skipping or reflection of light on the surface of water. My goal here is not to explain each and every example.

Viewing sine, cosine and tangent as percentages

(not to scale)

Another way to interpret the ratios is a percentage, because every ratio is a percentage. Sine, cosine and tangent assume values between 0 and 1, with the values between 0 and -1 being reflections. Now there is a mistake in here that is: a% + b% = 100% holds true for quantities that do not depend on direction. In other words, scalar quantities. Or in case we have just one dimension and vectors in one dimension. With vectors in 2D or 3D we can't do that division because it won't hold true. In Euclidean geometry we have to use the Pythagoras theorem.

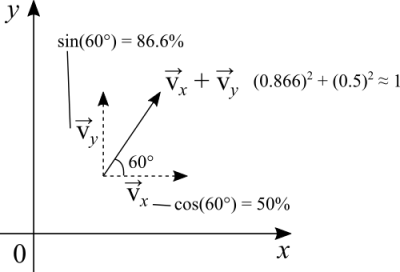
The above figure depicts a velocity vector and the angle 60°. As you can see, [math]\displaystyle{ \sin(60^{\text{o}}) = 0.866 }[/math] and [math]\displaystyle{ \cos(60^{\text{o}}) = 0.5 }[/math]. [math]\displaystyle{ 86.6% + 50% \gt 100% }[/math]. The mistake in this reasoning is that it really only works if we take one segment and divide it into two parts. What the percentages means is not exactly 86.6% of the velocity is contained in the vertical component, while the remaining 13.4% is contained in the horizontal component. The length of the vertical component is 86.6% of the length of the vector. The length of the horizontal component is 50% of the length of the vector.

The idea here is of vector projection. I think that due to the way we are taught algebra, we forget that to divide one number by another is the same thing as to calculate a ratio. For example: 5 / 4 = 1.25. In other words, the number 5 is 25% greater than 4. Because 4 times 1.25 is equal to 5. How many times does 4 units fit into 5 units? 1.25 times. The reversed thinking is: How much 4 is of 5? 4 is 80% of 5. Because the difference between 4 and 5 is one unit and one unit is 20% of 5. We can divide a vector into two parts, but this yields two parallel vectors. With projection what we do to a vector is to decompose it. It's very common to treat vectors as scalars and think that the sum of two vectors is done in the same way as we do to scalar quantities.