Definindo uma função
Uma função é uma regra que associa um conjunto de elementos com outro (há maneiras mais rigorosas de definir mas por agora basta isto). Temos um conjunto D onde cada um de seus elementos esta associato com outro elemento de um outro conjunto, o E. O conjunto D é chamado de Domínio da função e o conjunto E de contradomínio da função. Cada elemento de D é chamado de entrada ou variável independente e cada elemento de E é chamado de saída ou variável dependente.
Caso o termo dependente cause confusão quando temos uma função constante, isto é, uma função que produz o mesmo valor para qualquer entrada. A função constante só pode calcular um valor se uma variável de entrada existir, qualquer que seja. Sem valor de entrada a função não tem saída nenhuma.
Para várias variáveis a definição de função é a mesma. Exceto que agora temos uma questão adicional: as variáveis independentes são independentes entre si? Em cálculo sim. Mas podemos muito bem pensar em muitas situações onde as variáveis independentes guardam alguma dependência entre si. Para tudo que aprendemos em cálculo, [math]\displaystyle{ f(x,y) = x + y }[/math] por exemplo. Considerando o domínio da função, os valores de cada par [math]\displaystyle{ (x,y) }[/math] não tem nenhuma dependência entre uma variável e a outra. Em álgebra linear esta independência de variáveis é chamada de "independência linear".
(Não, a entrada e a saída não precisam ser do mesmo tipo)
A flecha é uma forma bem intuitiva de mostrar que os elementos de D são levados a elementos de E. Note que cada elemento de D deve corresponder a algum elemento de E. Se houver algum de D que não, então ele não faz parte do domínio. Note também que cada [math]\displaystyle{ x }[/math] corresponde a um [math]\displaystyle{ f(x) }[/math], o que significa que são todos pares ordenados [math]\displaystyle{ (x, \ f(x)) }[/math]. Ordenados porque, como a flecha indica, a direção importa. Você não pode simplesmente escrever um par em qualquer ordem porque fazendo isto você estará destruindo a relação dos elementos.
Notação: [math]\displaystyle{ f \ : D \ \to \ E }[/math]. Na maior parte do tempo não precisamos escrever isso e escrevemos apenas [math]\displaystyle{ f(x) = x^2 + 3x - 5 }[/math] porque é bastante óbvio pela própria equação que representa a função quais são os conjuntos D e E. Quando traçamos o gráfico de uma função não importa se o eixo vertical for chamado de [math]\displaystyle{ f(x) }[/math] ou [math]\displaystyle{ y }[/math]. Apenas é mais comum usar [math]\displaystyle{ x, \ y }[/math] para nomear os eixos (e [math]\displaystyle{ z }[/math] no caso de funções de duas variáveis).
A flecha pode ser invertida? Sim, este é o conceito da função inversa. Porém, nem toda função pode ser invertida e alguns processos não são reversíveis (há muitos exemplos de processos irreversíveis na física e na química). A condição para que uma função seja invertível é que para cada [math]\displaystyle{ f(x) }[/math], corresponde apenas um [math]\displaystyle{ x }[/math], tal que [math]\displaystyle{ x \to f(x) }[/math]. Em outras palavras, de [math]\displaystyle{ x }[/math] vamos à [math]\displaystyle{ f(x) }[/math] e vice-versa. Se acontecer isto [math]\displaystyle{ x_1, \ x_2 \to f(x) }[/math], é impossível saber a partir de [math]\displaystyle{ f(x) }[/math] se partimos de [math]\displaystyle{ x_1 }[/math] ou [math]\displaystyle{ x_2 }[/math]. Ou seja, a função não é invertível.
Uma questão natural sobre as funções inversas: não aprendemos o teorema na escola, mas podemos aprender o significado de uma função inversa. O que fazer no caso de funções de várias variáveis? O conceito é o mesmo, mas entra uma complicação. O domínio de uma função de uma variável (real) é um conjunto de números ordenados. O domínio de uma função de duas variáveis é um conjunto de pares ordenados. Com funções de várias variáveis há infinitos pares ordenados que são levados ao mesmo valor. O que fazer? Não é possível explicar aqui com um parágrafo só.
Uma analogia: suponha que tenhamos uma máquina que processa água, energia, açúcar, aromatizantes e glucose de milho para produzir doces. A máquina só produz doces. Não pode produzir, digamos, bolos com os mesmos ingredientes usados para produzir doces. Por outro lado, se introduzirmos sal, amido de milho e morangos na mesma máquina, ela não produzirá nada porque não foi feita para processar morangos, sal e amido de milho.
Sobre a terminologia: É muito comum o uso indistinto das palavras "parâmetro", "argumento" e "incógnita". Em grande parte das vezes elas significam a variável de entrada. Parâmetro é frequentemente encontrado em equações com interpretação geométrica, porque mudanças no valor do parâmetro mudam o tamanho de um círculo ou a inclinação de uma rampa por exemplo. Na física as variáveis frequentemente carregam um significado, como por exemplo mudar a taxa de variação de algo. Um exemplo prático seria uma equação que descreve a transparência de um material. Ele pode ser mais ou menos transparente e esta propriedade é controlada por um parâmetro. A palavra "argumento" é mais comum na matemática para se referir ao argumento de uma função. "Incógnita" por sua vez é sinônimo para "variável" na maioria das vezes. É mais comum quando temos que resolver equações ou sistemas de equações.
Contradomínio e imagem: nos livros em inglês de cálculo é muito comum o termo range para indicar as duas coisas. Em tradução livre seria a faixa de valores produzidos pela função. A palavra domínio não causa maiores problemas. Já contradomínio sim. Em inglês se diz codomínio em tradução livre. Em português o prefixo co foi substituído por contra por algum motivo. Temos o domínio que é o conjunto de entrada e o contradomínio que é o de saída, formando um par de conjuntos onde a função é o que liga os elementos de um ao outro. Quanto ao termo imagem, um dos livros que tenho define que, do par [math]\displaystyle{ (x, \ f(x)) }[/math], o segundo elemento é chamado de imagem do primeiro. Numa interpretação visual, [math]\displaystyle{ x }[/math] é o valor de entrada e [math]\displaystyle{ f(x) }[/math] é a saída que a função produz, algo que podemos ver, num gráfico por exemplo. O conjunto imagem e o contradomínio podem ter a mesma quantidade de elementos, mas a imagem nunca pode conter mais elementos do que o contradomínio. Um exemplo é [math]\displaystyle{ f(x) = x^2 }[/math]. É uma função de valores reais a valores reais. O contradomínio são todos os reais, mas a função não produz números negativos. A imagem é [math]\displaystyle{ \mathbb{R}_*^{+} }[/math].
| Examplos | |
|---|---|
 |
Suponha que temos uma função que aceita qualquer número real como entrada e na saída produz a constante 2. A saída é sempre 2 e nada mais ou menos. O número 4 não pode fazer parte da imagem desta função, mas pode fazer parte do contradomínio. |
 |
Agora o problema oposto. Suponha que uma função produz como saída a raiz quadrada de um número real. O que acontece se a entrada for -1? A raiz quadrada de -1 é um número complexo e como a função esta definida para valores reais, nada acontece. Não existe a raiz quadrada de -1 nos reais. Logo, -1 não faz parte do domínio da função. |
 |
Pode uma função levar um elemento e mais do que um outro elemento? É impossível! É por isto que o gráfico de uma função não pode formar um laço. O gráfico de uma função de duas variáveis não pode ser uma esfera ou um cilindro. Pense numa situação real. Pode o mesmo ponto do espaço, ao mesmo tempo, ter duas temperaturas diferentes? Pode o mesmo objeto, num certo instante de tempo e numa certa posição no espaço, ter dois valores de massa diferentes? Não vamos entrar na discussão filosófica do significado das medidas.
Se uma função modular tiver casos sobrepostos esta errado. Se for um algoritmo num computador, o mais comum é a execução do primeiro caso satisfeito. |
 |
Métodos numéricos: frequentemente temos dados experimentais na forma de pontos com pares de coordenadas [math]\displaystyle{ (x,y) }[/math]. Às vezes não há um padrão óbvio e os dados parecem aleatórios. Porém, se os pontos mostram um padrão, provavelmente há uma função e para descobrir qual é temos que recorrer aos métodos numéricos para encontrar a melhor função para aquele caso. Dependendo do caso precisamos dividir o gráficos em partes menores porque apenas uma função não vai conseguir descrever todos os pontos, mas cada parte é uma função diferente.
A estatística também tem a sua parte na aproximação de funções porque sempre há um erro associado com cada medida. Medidas sem erros não existem. Dados do mundo real nunca se encaixam perfeitamente numa curva, o que significa que na maior parte das vezes estamos desconsiderando algumas variações de alta frequência. Uma questão interessante é se a função precisa ser uma só e, se for modular, o que acontece com os valores que separam uma parte da função da próxima. A resposta depende muito do experimento que você esta conduzindo. Pode ser ou não necessário, ou mesmo viável, uma "ampliação" ao redor de tais pontos para capturar o máximo de detalhes. Resolver numericamente ou analiticamente? O primeiro significa calcular um valor numérico com uma aproximação boa o bastante da solução verdadeira, o valor teórico. O segundo significa achar uma solução exata ou uma fórmula. |
Physical interpretation: We are often not interested in all values of a function but just a particular range. For example: a function may represent volume in respect to something. The function itself can assume negative values. However, a negative volume doesn't exist. Another example: speed over time. Due to the laws of physics, speed can't be an infinitely large quantity, there is the upper limit of the speed of light. We can, nonetheless, plot the graph. It just won't have any physical meaning beyond the speed of light. That's where pure math comes in, where the physical meaning of a function is lost.
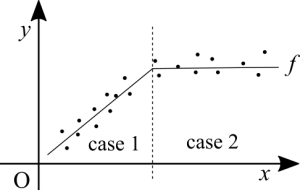
Functions from data points: in Calculus, most of the time, you are given the function. In many scenarios the function is unknown. What is known is the data. If the data is nicely ordered on a table, numerical patterns may be quickly noticed. Easy patterns such as periodic oscillations, increasing at a constant rate, at an exponential rate or decreasing exponentially. If an easy pattern cannot be identified, you'd have to plot the data on the Cartesian plane to see if there is any noticeable pattern. This is more or less an exercise of guessing which of the known functions seems to best approximate the data's behaviour.
In experimental physics, most of the time you already know the function. The classes aren't about trying to guess which function is it. The experiments done already give you the function and the goal of it is more about testing the limits in which that function remains a good approximation for the data that you gather. In those experiments there are tiny bits of statistics because there is some error analysis to be performed on the data.
In practical terms, data can also display bizarre behaviour, in which case one's knowledge about the phenomena is what makes those bizarre behaviours to be spotted. For example: the speed of sound in air is known. If there is a table and one point depicts an excessively high speed. It either means that the data itself is wrong due to some collection error or that somebody inserted data that shouldn't have been there. For statistics those points may be relevant, such as whether they represent an error or a spike. A spike in crime rates for instance?
