Completing the square and the quadratic formula

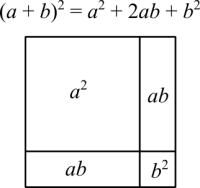
Completing the square is best viewed with a geometric perspective. First let me show a figure:

The graphical association is pretty clear. What, sometimes, is not very obvious, is the fact that [math]\displaystyle{ (a + b)^2 }[/math] can be seen as literal. The whole square has its side given by a sum of two shorter sides, [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math].

The idea of completing the square is to rewrite quadratic equations in a form that has a term in the form [math]\displaystyle{ (a + b)^2 }[/math]. We all learn at school that quadratic equations have this form [math]\displaystyle{ ax^2 + bx + c }[/math]. When [math]\displaystyle{ c = 0 }[/math] it's easy to calculate the roots because we can factor out in the form [math]\displaystyle{ x(ax + b) }[/math]. Then we solve a linear equation. If we have an equation with the form [math]\displaystyle{ ax^2 + bx }[/math] it's really the same as [math]\displaystyle{ a^2 + ab }[/math] as the figure above shows. The problem is that it's missing [math]\displaystyle{ ab + b^2 }[/math]. To complete the square means to find those two missing terms.

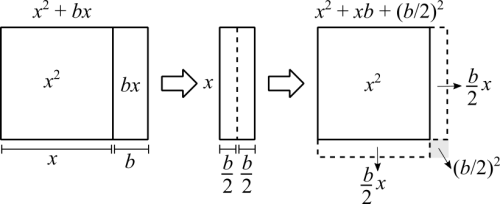
Graphically, we have this:

[math]\displaystyle{ x^2 + bx = \left(x + \frac{b}{2}\right)^2 }[/math] (We didn't change the area. We just rearranged it. What was a rectangle is now a perfect square)

It's kinda funny how most textbooks mention this topic without making the association with the squares. Squares, literally squares.

Reference: I have seen all that graphical reasoning in the site mathisfun.

Bhaskara's Formula: I have no idea why in Brazil the formula to solve quadratic equations bears that name, while other countries in the world do not make that association with quadratic equations and that Indian mathematician. Another curious fact is that there are two mathematicians with that name and most people don't know that. One lived thousands of years before Christ, the other hundreds of years after Christ.