Linear approximation for one variable

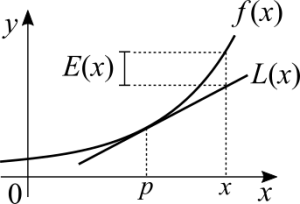
Most textbooks explain the idea of finding the tangent line at a certain point of a function. The geometric idea is that if you consider a very small interval, the function can be approximated by a linear function. Linear means a constant rate of change. Some textbooks give the idea of zooming in a function's graph. If we take a parabola and zoom in enough, a small piece of it should be rendered as a straight line on a computer's screen. That's the whole geometric idea of the derivative.

(not to scale)

With calculus we are always plotting graphs over an euclidean space. In euclidean geometry the shortest distance between two points is always a straight line. This is one reason to explain why we have the problem of finding a tangent line. Between two points we have infinitely many paths, but among all of them there is one that is a straight line and it happens to minimize the distance travelled between the two points. Not every teacher mentions this and there is also a problem of schedule. Time is often too short to teach this.

It's clear that the tangent line is a good approximation of the function if we consider a certain margin of error. The graph clearly shows that beyond a certain margin the error is too great. One way to think about it is to consider how hard it is to calculate the value of a function. It may be feasible to consider that between two points we can disregard the precision and use a function that is easier or faster to calculate.