Aproximação linear para uma variável

A maioria dos livros explicam o problema de achar a reta tangente num certo ponto de uma função. A ideia geométrica por trás da derivada é a de que, se a função for diferenciável, então podemos aproximá-la por uma função linear. Alguns livros dão a ideia de ampliar a imagem como um microscópio faz para ver coisas muito pequenas. Quando dois pontos da função são muito próximos um do outro podemos considerar uma taxa de variação média entre eles. Numericamente significa aceitar uma margem de erro em troca de perdermos precisão ao considerarmos uma função mais simples entre dois pontos, a fim de simplificar cálculos. No caso da reta tangente o que se tem é, que entre dois pontos, podemos considerar uma taxa de variação constante.

(sem escala)

With calculus we are always plotting graphs over an euclidean space. In euclidean geometry the shortest distance between two points is always a straight line. This is one reason to explain why we have the problem of finding a tangent line. Between two points we have infinitely many paths, but among all of them there is one that is a straight line and it happens to minimize the distance travelled between the two points. Not every teacher mentions this and there is also a problem of schedule. Time is often too short to teach this.

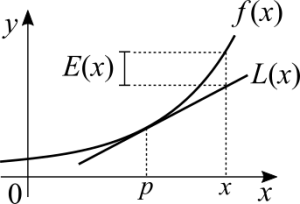
It's clear that the tangent line is a good approximation of the function if we consider a certain margin of error. The graph clearly shows that beyond a certain margin the error is too great. One way to think about it is to consider how hard it is to calculate the value of a function. It may be feasible to consider that between two points we can accept a certain margin of error and use a function that is easier or faster to calculate. In numerical methods we have a more thoughtful discussion about this because we want to answer the question "How close do we have to be from the real value? Is there a limit for the error?".

With analytical geometry we can find the equation of line if we know two points or one point and the angular coefficient. The same concept applies to finding functions that pass through points. With the derivative's definition we can find the affine function that approximates a function with a very simple algebraic manipulation:

[math]\displaystyle{ \frac{f(x) - f(p)}{x - p} = f'(p) }[/math]

[math]\displaystyle{ f(x) = f(p) + f'(p)(x - p) }[/math] (Remember that [math]\displaystyle{ x - p \neq 0 }[/math])

Notice that in the above graph there is an [math]\displaystyle{ E(x) }[/math] that represents the difference between the affine function and the function itself. Therefore:

[math]\displaystyle{ L(x) = f(p) + f'(p)(x - p) + E(x) }[/math]

The best approximation in this case happens when [math]\displaystyle{ E(x) = 0 }[/math], which means that we are as close as possible to the function we are approximating.

Not every function is going to be easier to calculate this way. First there is a problem with differentiability. If the function can't be differentiated we can't use the linear approximation. Second, trading a sine by a cosine or vice-versa isn't going to make our lives any easier or harder.