Visualising the domain of a function

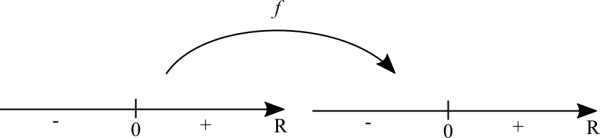
For functions of one variable the domain of a function is quite easy to plot. It's a number line. The function takes elements from the number line, processes them and produces another number line. For most of the time in a calculus course we are concerned with the real numbers. Complex numbers are usually left to a later stage.

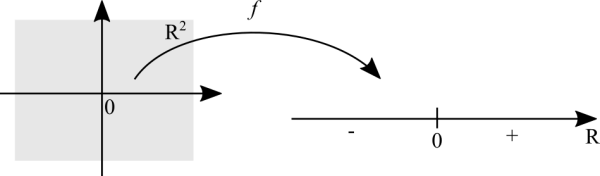
For two variables we are considering the whole Cartesian plane and all pairs (x,y) in it. For three variables it's all points (x,y,z) from the 3D space and then it's not practical to plot by hand. For four or more variables it's the hyperspace, impossible to view.

The domain of a function of two variables can resemble the graph of a function of one variable. However, graphs of single variable functions are always 1D, in the sense that they are lines with zero thickness. A single variable function can never plot any 2D shape with an area. By analogy, the domain of a function of three variables is contained in the 3D space. Functions of two variables can plot sheets, surfaces, planes, but never all points inside a sphere, cube or a cone for example.

A simple way to imagine the domain of a function of one or two variables is to picture a shadow. Under one specific condition, the imaginary light source is perpendicular to the XY plane and all light rays are parallel to each other. What's the shadow of a cable? A thin line. What's the shadow of half a spherical dome? A circle. Careful, we are considering the projected shadow over a flat surface, not the whole space that is obscured by the cable or the dome. Notice that if we //stretch// or //squeeze// the graph vertically, the shadow keeps the same shape. The shadow also disregards any irregularities or oscillations in between the extreme points or edges. That same idea can be extended to higher dimensions. A 4D object projects a 3D shadow for example.

In the computer graphics world the idea of projected shadows is the basic concept behind rendering lights and shadows. We evaluate which points are being hit by a light ray and which ones aren't. Under the simplest model, either a surface allows light to pass or not.

Note: from what I remember from school, I think no teacher ever complained about using ":" or "|".

Examples for one variable

[math]\displaystyle{ f(x) = x^2 }[/math]. There is no restriction to which numbers we can calculate the square of. Any rational or irrational will do. i.e. The domain is all real numbers.

[math]\displaystyle{ f(x) = \sqrt{x} }[/math]. We all learn at school that roots of negative numbers are complex numbers. Therefore, the domain is [math]\displaystyle{ \{x \in \mathbb{R} : x \geq 0\} }[/math]

[math]\displaystyle{ f(x) = 1/x }[/math]. There is only one concern that is the division by zero. Excluding the [math]\displaystyle{ x }[/math] for which we would have a division by zero, the domain is everything else. i.e. [math]\displaystyle{ \{x \in \mathbb{R} : x \neq 0\} }[/math]

[math]\displaystyle{ f(x) = \log(x) }[/math] or [math]\displaystyle{ f(x) = \ln(x) }[/math]. When log is written without a base, it's assumed that the base is [math]\displaystyle{ e }[/math]. The Euler's number. It's an irrational number 2.71... Logarithm is defined as the inverse of an exponential [math]\displaystyle{ \log_ba = x \iff b^x = a }[/math]. When we have powers it's impossible to generate negative numbers or the zero. Therefore, the domain is [math]\displaystyle{ \{x \in \mathbb{R} : x \gt 0\} }[/math].

[math]\displaystyle{ f(x) = x^x }[/math]. First, [math]\displaystyle{ 0^0 }[/math] is undefined, there is no value for it. For any positive number we have rationals and irrationals, any positive number works. But what happens when the exponent it's a rational number? Then [math]\displaystyle{ x^{1/2} = \sqrt{x} }[/math]. What if [math]\displaystyle{ x \lt 0 \ ? }[/math] Then we have a tricky situation. [math]\displaystyle{ (-2)^{-2} = 1/(-2)^2 = 1/4 }[/math]. For integers, no problems. What about rationals? [math]\displaystyle{ (-1/2)^{-1/2} = -1/\sqrt{-1/2} }[/math]. Now we have a complex number. The function does exist for negative inputs, but it's going to be a series of disconnected points because there are always rationals in between two integers. Therefore, domain is [math]\displaystyle{ \{x \in \mathbb{R} : x \gt 0\} }[/math] to simplify calculations.

[math]\displaystyle{ f(g(x)) }[/math]. First, look for the domain of [math]\displaystyle{ g(x) }[/math]. If there are no restrictions, then all reals are part of this function's domain. What about [math]\displaystyle{ f(x) \ ? }[/math] Some values that [math]\displaystyle{ g }[/math] calculate may be forbidden for [math]\displaystyle{ f }[/math], but the function that "governs" the domain is [math]\displaystyle{ g }[/math] because any input goes in it first.

[math]\displaystyle{ f(x) = \sqrt{|x|} }[/math]. The domain is all reals, but let's look at it as a piecewise function. For [math]\displaystyle{ x \gt 0 }[/math] we can ignore the modulus and treat it as [math]\displaystyle{ \sqrt{x} }[/math]. For [math]\displaystyle{ x \lt 0 }[/math] we have that [math]\displaystyle{ |-x| = x }[/math]. Therefore, a more precise way to define the domain is as the union of two sets, [math]\displaystyle{ \mathbb{R}^{-} \cup \mathbb{R}_ {*}^{+} }[/math].

Examples for two variables:

	[math]\displaystyle{ f(x,y) = xy }[/math]. Both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] can assume any real value. Therefore the domain is [math]\displaystyle{ \mathbb{R}^2 }[/math].
	[math]\displaystyle{ f(x,y) = \sqrt{x} + \sqrt{y} }[/math]. It's analogous to a single variable. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \geq 0 \ \text{and} \ y \geq 0\} }[/math].
	[math]\displaystyle{ f(x,y) = \sqrt{x + y} }[/math]. How many solutions do we have for [math]\displaystyle{ x + y \lt 0 \ ? }[/math] Infinite. We want to exclude all pairs that obey both [math]\displaystyle{ x \lt -y }[/math] and [math]\displaystyle{ y \lt -x }[/math] from the Cartesian plane. Where [math]\displaystyle{ x = y \ ? }[/math] [math]\displaystyle{ f(x) = x }[/math]. Where [math]\displaystyle{ x = -y \ ? }[/math] [math]\displaystyle{ f(x) = -x }[/math]. We want to exclude all [math]\displaystyle{ (x,y) }[/math] that are to the left and below [math]\displaystyle{ f(x) = -x }[/math]. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x + y \geq 0 \} }[/math]
	[math]\displaystyle{ f(x,y) = \sqrt{9 - x^2 - y^2} }[/math]. When we have composite functions like this we have to think on the graph of each nested function. For which values we have [math]\displaystyle{ 9 - x^2 - y^2 \lt 0 \ ? }[/math] That inequality leads to [math]\displaystyle{ x^2 + y^2 \gt 9 }[/math]. That does resemble the equation of a circle with [math]\displaystyle{ r = 3 }[/math]. Except that the inequality represents all points outside the circle. Therefore, for [math]\displaystyle{ x^2 + y^2 \gt 9 }[/math] we have all points for which the square root of a negative number is not part of this function's domain. We want the opposite, so [math]\displaystyle{ x^2 + y^2 \leq 9 }[/math] represents all points inside the circle, including the perimeter. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x^2 + y^2 \leq 9\} }[/math]
	[math]\displaystyle{ f(x,y) = \ln(x - y^2) }[/math]. Log of zero or negative doesn't exist. So, for which values [math]\displaystyle{ x - y^2 \gt 0 \ ? }[/math] We want all pairs obeying to [math]\displaystyle{ x \gt y^2 }[/math]. Remember that [math]\displaystyle{ f(x) = y }[/math], so [math]\displaystyle{ f(x) = \sqrt{x} }[/math] or [math]\displaystyle{ f(x) = -\sqrt{x} }[/math]. All points that are in between, excluding the frontier, the graphs of [math]\displaystyle{ f(x) = \sqrt{x} }[/math] and [math]\displaystyle{ f(x) = -\sqrt{x} }[/math] are the points that we want. Notice how the domain resembles a parabola rotated 90° clockwise. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \gt y^2\} }[/math]
	[math]\displaystyle{ f(x,y) = 1/(x + y) }[/math]. This is easy. To avoid the division by zero we want all pairs where [math]\displaystyle{ x \neq -y }[/math] and [math]\displaystyle{ -x \neq y }[/math]. In other words, every pair which doesn't obey [math]\displaystyle{ f(x) = -x }[/math]. Domain is [math]\displaystyle{ \{(x, \ y) \in \mathbb{R}^2 : x \neq -y \ \ \text{and} \ -x \neq y\} }[/math]