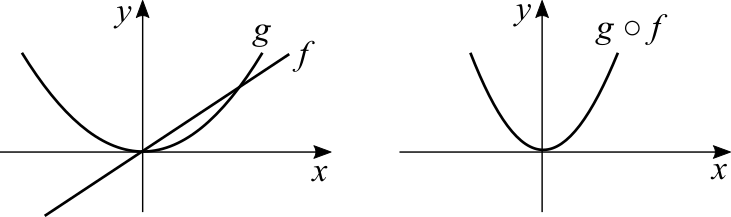Regra da cadeia para funções de uma variável
A regra da cadeia é, intuitivamente, um produto de duas derivadas. Suponha que temos três objetos móveis: A, B e C e que suas respectivas velocidades são A > B > C. Se soubermos quantas vezes a velocidade de A é maior em relação à B e B em relação à C, então podemos saber quantas vezes A é maior em relação à C também. O que precisamos fazer é multiplicar a razão entre A e B pela razão entre B e C. Este exemplo esta em Artigo (em inglês) na Wikipedia.
Outro exemplo. Na meteorologia temos a Lapse rate (taxa vertical de variação da temperatura) que é a variação da temperatura em relação à altura na atmosfera. É uma razão °C / km. Se voarmos para cima ou para baixo sentimos mudanças na temperatura porque estamos nos deslocando em relação a cada nível de temperatura na atmosfera. O oposto disto não acontece porque se ficarmos parados a atmosfera não será subir ou descer em relação a nós. Voando mais rápido naturalmente resulta em mudanças mais rápidas de temperatura. Nossa velocidade é uma razão km / tempo. Se quisermos a razão °C / tempo precisamos calcular o produto [math]\displaystyle{ \frac{^{\text{o}}C}{km} \frac{km}{time} = \frac{^{\text{o}}C}{time} }[/math].
[math]\displaystyle{ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} }[/math]
É importante ressaltar uma coisa: o exemplo acima da temperatura atmosférica é um caso linear (assumindo que voamos a uma velocidade constante), que se traduz em [math]\displaystyle{ T_1'(t) = T_2'(h) \cdot h'(t) }[/math]. Onde [math]\displaystyle{ T_1'(t) }[/math] é a variação da temperatura pelo tempo e o lado direito é o produto da variação da temperatura pela altura pela variação da altura pelo tempo. Perceba que a função inserida em [math]\displaystyle{ T_2'(h) }[/math] é a função que dá a razão altura / tempo. Perceba que existem duas taxas de variação diferentes.
[math]\displaystyle{ h'(x) = g'(x) \cdot f'(g(x)) }[/math]
Podemos ter qualquer quantidade de funções inseridas uma na outra. A regra continua válida e o nome advém do fato de que temos uma corrente de operações, uma corrente de derivadas.
Observação: às vezes temos funções compostas mas não as vemos claramente. Por exemplo: [math]\displaystyle{ y = \sen^2(x) }[/math]. É claro que temos um produto [math]\displaystyle{ y = \sen(x) \sen(x) }[/math], mas também poderíamos ver assim [math]\displaystyle{ y = x^2 }[/math] e [math]\displaystyle{ x = \sen(x) }[/math]. Numa notação mais convencional: [math]\displaystyle{ f(x) = x^2 }[/math], [math]\displaystyle{ g(x) = \sen(x) }[/math] e [math]\displaystyle{ f \circ g = \sen^2(x) }[/math]. Isto é especialmente comum com a diferenciação implícita.
Raciocínio gráfico para a regra da cadeia
Eu não conheço livros que mostrem uma interpretação gráfica para a regra da cadeia. Vamos considerar [math]\displaystyle{ f(x) = 3x }[/math] e [math]\displaystyle{ g(x) = x^2 }[/math]. O gráfico da primeira é uma reta e a constante é o coeficiente angular, onde maior significa uma inclinação maior. A segunda é uma parábola. A primeira tem uma taxa de variação constante, enquanto a segunda não tem uma taxa constante.
O gráfico de [math]\displaystyle{ g(f(x)) = (3x)^2 }[/math] tem uma taxa de variação maior do que o gráfico de [math]\displaystyle{ g(x) = x^2 }[/math]. Pense sobre isto: se escolhermos [math]\displaystyle{ x = 2 }[/math] as taxas de variação são, naquele ponto e para cada função, [math]\displaystyle{ f'(2) = 6 }[/math] e [math]\displaystyle{ g'(2) = 4 }[/math]. Para a função composta temos [math]\displaystyle{ g'(f(x)) = f'(2)g'(f(2)) = 6 \cdot 2 \cdot 3 = 36 }[/math]. Eu fiz um exemplo com números positivos mas a regra da cadeia vale para negativos e também para funções mais complicadas.
Observação: in this specific case we could have used the product rule. Or even faster, the power rule.
Proof of the chain rule
It's natural to think that the derivative of the composite function is the composition of the derivatives. It's the same intuition that commonly happens with the product and quotient rules. When we have a composition, one function is the dependent variable of the other. We can be easily fooled and think that the derivative of [math]\displaystyle{ f(g(x)) }[/math] is [math]\displaystyle{ f'(g'(x)) }[/math]. Mathematically this doesn't make sense because we just swapped a function by its derivative. Who said that it's right to replace a function by its derivative and expect the result of this operation to be meaningful? Who said that the rate of change of [math]\displaystyle{ f }[/math] depends on the rate of change of [math]\displaystyle{ g }[/math]?
The problem of finding the tangent line describes how a differentiable function can be seen as a linear function if we consider a small enough interval around a point. Let's begin by defining two affine functions:
[math]\displaystyle{ f(x) = ax + b }[/math]
[math]\displaystyle{ g(x) = cx + d }[/math]
Let's take a look at:
[math]\displaystyle{ f(g(x)) = ag(x) + b }[/math]
[math]\displaystyle{ f(cx + d) = a(cx + d) + b }[/math]
[math]\displaystyle{ f \circ g = acx + ad + b }[/math]
Did you notice the product between the angular coefficients, [math]\displaystyle{ a \cdot c }[/math]? If we differentiate the expression [math]\displaystyle{ acx + ad + b }[/math] in respect to [math]\displaystyle{ x }[/math], the operation yields [math]\displaystyle{ ac }[/math]! Surprise! That's not a formal proof though. The fundamental idea behind it is that if the function is differentiable, then near some point of it we can treat it as a linear function.
Links for the proof: