Completing the square and the quadratic formula

Completing the square is best viewed with a geometric perspective. First let me show a figure:

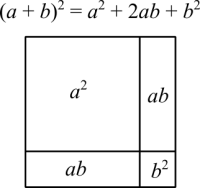
The graphical association is pretty clear. What, sometimes, is not very obvious, is the fact that [math]\displaystyle{ (a + b)^2 }[/math] can be seen as literal. The whole square has its side given by a sum of two shorter sides, [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math].

The idea of completing the square is to rewrite quadratic equations in a form that has a term in the form [math]\displaystyle{ (a + b)^2 }[/math]. We all learn at school that quadratic equations have this form [math]\displaystyle{ ax^2 + bx + c }[/math]. When [math]\displaystyle{ c = 0 }[/math] it's easy to calculate the roots because we can factor out in the form [math]\displaystyle{ x(ax + b) }[/math]. Then we solve a linear equation. If we have an equation with the form [math]\displaystyle{ x^2 + bx }[/math] it's really the same as [math]\displaystyle{ a^2 + ab }[/math] as the figure above shows.

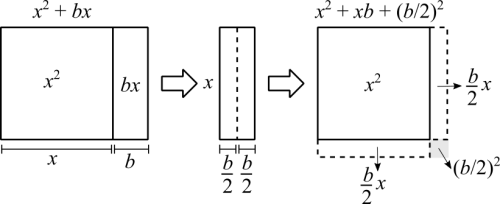
Graphically, we have this:

[math]\displaystyle{ x^2 + bx + \left(\frac{b}{2}\right)^2 = \left(x + \frac{b}{2}\right)^2 }[/math] (Notice that to complete the square we did increase the total area)

It's kinda funny how most textbooks mention this topic without making the association with the squares. Squares, literally squares.

Reference: I have seen all that graphical reasoning in the site mathisfun.

Proof of the formula to solve 2nd degree polynomial equations

We can use the process of completing the squares to find a formula to solve quadratic equations. Try to isolate [math]\displaystyle{ x }[/math] in [math]\displaystyle{ ax^2 + bx + c = 0 }[/math]. You are quickly going to see that, due to the equation having both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ x^2 }[/math], it's going to be hard to achieve it. We really have to rewrite the equation to successfully isolate [math]\displaystyle{ x }[/math]. Look back at the previous figure, the only difference between [math]\displaystyle{ ax^2 + bx + c }[/math] and [math]\displaystyle{ x^2 + bx }[/math] is that we have a constant multiplying the square (making it larger or smaller) and a lonely constant.

The previous example increased the area of the square. Now let's impose a condition. We want to complete the square but not change the total area of the figure. The question is: the first term is already a perfect square, can the extra rectangle be divided into two equal parts plus one small square? Or, from a different perspective, divide the rectangle into four smaller rectangles and four smaller squares.

1st we can divide everything by [math]\displaystyle{ a }[/math] because if [math]\displaystyle{ a = 0 }[/math] we no longer have a quadratic equation (Why not [math]\displaystyle{ b }[/math] or [math]\displaystyle{ c }[/math]? Because they can be zero and the equation remains quadratic):

[math]\displaystyle{ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \iff x^2 + \frac{b}{a}x = -\frac{c}{a} }[/math] (looking back, we have that [math]\displaystyle{ b/a }[/math] is one of the sides of the rectangle)

[math]\displaystyle{ x^2 + \frac{b}{2a}x + \frac{b}{2a}x = -\frac{c}{a} }[/math] (see where the [math]\displaystyle{ 2a }[/math] shows up in the formula that we learn at school? We divided the rectangle in two)

From here we want to have a perfect square as in the previous figure. Let's look at the left side and ignore the right side for a moment:

[math]\displaystyle{ x^2 + \frac{b}{2a}x = x\left(x + \frac{b}{2a}\right) }[/math] (we got close, but there is that wild [math]\displaystyle{ x }[/math] making our lives harder)

[math]\displaystyle{ x^2 + \frac{b}{2a}x = x\left(x + \frac{b}{2a}\right) }[/math]

Bhaskara's Formula: I have no idea why in Brazil the formula to solve quadratic equations bears that name, while other countries in the world do not make that association with quadratic equations and that Indian mathematician. Another curious fact is that there are two mathematicians with that name and most people don't know that. One lived thousands of years before Christ, the other hundreds of years after Christ.

Completing the cube: one may have wondered if the same procedure can work for cubes. The geometric idea is quite applicable. However, we have to impose a certain condition. The cubic equation must be such that it only has one root, the cubic root.