Formal limit and continuity of a single variable function
I have a textbook which begins with the definition of continuity and another book that defines limit first. There are some textbooks that begin with derivatives and there is one (Tom M. Apostol) that chooses to begin with integration. I'll begin with limits for no special reason. People can read sites in any order they want so I don't think it matters that much.
Discussion of limits
(not to scale)
What does it mean to calculate a limit? The intuitive idea of a limit is that of a boundary. At some point in school we learn to solve inequalities and the answers are usually a range of values, such as [1, 7] or ]0, 2[. A closed interval means that the variable can assume any value close to it, including the boundary value itself. An open interval means that the variable can assume any value close to it, except for the boundary value itself. Another way to see it. Suppose we take a number and divide it by 2 and repeat it as many times as we want to. We know that it'll get smaller and smaller but not past zero. That's the intuitive notion of a limit.
Now for the notation:
[math]\displaystyle{ \lim_{x \ \to \ a} f(x) = L }[/math]
As [math]\displaystyle{ x }[/math] approaches, gets near, [math]\displaystyle{ a }[/math]. [math]\displaystyle{ f(x) }[/math] approaches, gets near, [math]\displaystyle{ L }[/math]. For this level of calculus what we are doing is inputting variables closer and closer to [math]\displaystyle{ a }[/math] and seeing what happens to [math]\displaystyle{ f(x) }[/math]. If the limit is converging to [math]\displaystyle{ f(a) }[/math]. Then great, we can calculate the value of the function there and it's going to be equal to the limit. Else, it's diverging to some other value, then we have some form of fracture in the function's graph. Not quite the most rigorous way, but it suffices for now. A natural question that may arise here: what about the speed at which we are getting closer to [math]\displaystyle{ a \ ? }[/math] That's more a physics concern than a mathematical one. In calculus our only concern is whether that limit exists or not. That point being reachable or not is another problem.
Some exercises try to trick us with a piecewise function. Suppose that one case defines the function for [math]\displaystyle{ f(0) = 0 }[/math]. The other case defines that the function obeys [math]\displaystyle{ f(x) = 1/x }[/math]. What happens if we calculate the limit as [math]\displaystyle{ x \ \to \ 0 \ ? }[/math] Don't be fooled by [math]\displaystyle{ f(0) = 0 \ !! }[/math] The limit is taking the independent variable as close as we want to zero, but just one small step away from it.
Limits of intuition: (pun) the hardest limits to calculate are those that defy intuition. For example: [math]\displaystyle{ \lim_{x \to 0} \ (\sqrt{x^2 + 9} - 3)/x^2 }[/math]. If we apply [math]\displaystyle{ x = 10^{-10} }[/math], the value seems to converge to zero. But if we solve the limit analytically, not numerically, the result should be [math]\displaystyle{ 1/6 }[/math]. Machines don't have infinite precision, the error comes from [math]\displaystyle{ \sqrt{9.000...1} = 3 }[/math]. Rounding errors is one of the fundamental problems of numerical methods.
The other case that defies intuition are limits that don't exit and yet are somewhere in between known values. That's the case of [math]\displaystyle{ \sin(1/x) }[/math] for example. We know that [math]\displaystyle{ -1 \lt \sin(x) \lt 1 }[/math]. When [math]\displaystyle{ x \to 0 }[/math], [math]\displaystyle{ \sin(1/x) }[/math] can assume any value between -1 and 1, it never converges to a certain fixed value. We know that the function is bounded between two fixed values, but in between them it never "stays still". This concept is important. When we have products of functions and one of them is bounded, we know that whatever value the bounded function assumes, it's not infinity. When we do that we are, in fact, relying on the squeeze theorem.
Discussion of continuity
What does it mean for something to be continuous? Without resorting to a precise mathematical definition, the property of being continuous means that something doesn't have gaps or fractures in between it's beginning and ending points. Think about water. At school we learn that water, down to the molecular level, is composed of a large number of molecules. Water is a continuous fluid, there is no space in between molecules of water (I'm disregarding any measures of the size of atoms or molecules). Now snow is still composed of water, however there is a lot of free space in between snowflakes. Snow is not continuous. Now let's think about rain. We can say "it's been continuously raining for days". Water, in the form of water droplets, is discontinuous. For the purposes of daily life we don't need a precise definition of continuity. For the purposes of math we do need a definition that doesn't allow us to confuse continuity with discontinuity.
Graph A is of a continuous function. Graph B is of a discontinuous function. Now be careful! Being continuous does not mean the same thing as being smooth. Look at the graph of [math]\displaystyle{ f(x) = |x| }[/math] at the origin is not a smooth curve, but it's continuous. The opposite can also happen, a function that is a straight line and yet is discontinuous at some point. Example: [math]\displaystyle{ f(x) = \frac{x^2 - 1}{x - 1} }[/math] has an obvious point where a division by zero occurs, yet the graph is a continuous straight line. We can think about discontinuity in terms of physics. Suppose an object at t = 1s has a velocity of 10 m/s. Now at t = 1.0000...1s the velocity has changed to 1000 m/s. Is it physically possible for the velocity of object to change that much in that little time? Infinite acceleration doesn't exist and that would equate to [math]\displaystyle{ \tan(\pi/2) }[/math] in this case. We've just discussed the concept of a derivative, which is a special case of a limit.
A natural question arises when we think about continuity. A function can be discontinuous at some point. Can we have a function that is discontinuous at every point? Such function exists and is easy to define. Let it be a piecewise function where [math]\displaystyle{ x }[/math] can assume the values 1 or 0, depending on whether [math]\displaystyle{ x }[/math] is rational or irrational. Without going through proofs, suppose we have the numbers [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] with [math]\displaystyle{ b \gt a }[/math]. Suppose that [math]\displaystyle{ a }[/math] is rational. Is [math]\displaystyle{ b }[/math] rational or irrational? We can prove that in between two rational numbers there is always some irrational number. The opposite is also true, in between two irrational numbers there must be some rational number. That means that in between two points of that function there is a always a gap, the function is never continuous. No matter how small the difference between two rationals or two irrationals is, we can't have two consecutive rationals or two consecutive irrationals.
An informal discussion for the above theorem: take the number [math]\displaystyle{ \pi }[/math]. Now add one. Now we have two irrationals, 3.14... and 4.14... Which rational can be in between? 3.5 for example. Now, can you see that in between 3.14... and 3.5 there must be infinitely many rationals and irrationals? In between any two rationals or irrationals we can keep subdividing into even smaller intervals and still find a number in between. We are disregarding the question of whether there are more rationals or more irrationals. Counting elements of a set is a different matter.
Can a function have many many points in which it's discontinuous but no everywhere as the example above? Divide a function by a sine or cosine, every time we get to divide by zero the function is going to be undefined. That is a function with an infinite quantity of discontinuities, yet not everywhere. It's still a continuous function if we consider its domain.
A question regarding continuity: is this or that function continuous? Are we talking about the whole set of all real numbers or just its domain (a subset of all reals)? This question arises quite often because when we say that a function is continuous is not exactly the same thing as to say that the function does not have any discontinuities. Take that example above of a function that is discontinuous everywhere. In that specific case, to say that it's not continuous is a synonym.
Introducing two sided limits
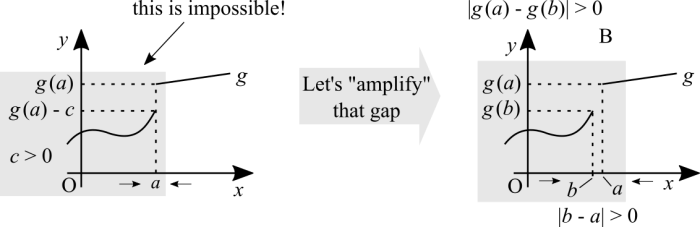
See how [math]\displaystyle{ g(a) \neq g(a) - c }[/math] contradicts that [math]\displaystyle{ a }[/math] is one, and only one, argument and [math]\displaystyle{ c \gt 0 }[/math]. This can only mean that there are two arguments, but they are so close to each other that the wrong graph "fused" them into one. The graph is intentionally wrong and exaggerated to show that a function cannot have two different values for the same argument. It violates the definition of a function. If we "zoom in" enough, we can see that there is a small gap in between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math]. That's how many teachers and textbooks that I know explain what it means for a function to be discontinuous at a point.
Suppose that the distance between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] is something very small but not null. If we choose any [math]\displaystyle{ x \lt b }[/math], the limit is converging to [math]\displaystyle{ g(b) }[/math]. If we choose any [math]\displaystyle{ x \gt a }[/math], the limit is converging to [math]\displaystyle{ g(a) }[/math]. With [math]\displaystyle{ g(a) \neq g(b) }[/math] we can only conclude that the function is discontinuous there.
Now we can write limits with an additional concept:
[math]\displaystyle{ \lim_{x \ \to \ a^+} f(x) = L_{1} }[/math]
[math]\displaystyle{ \lim_{x \ \to \ a^-} f(x) = L_{2} }[/math]
We are calculating limits but now we care about the path. We can approach [math]\displaystyle{ a }[/math] from the left or from the right. If both paths converge to the same value, then the limit exists. Otherwise, if [math]\displaystyle{ L_1 \neq L_2 }[/math] the limit doesn't exist at that point.
What's the difference between a limit and a two sided limit? Conceptually, none. It's just that the first is a general idea and the second splits that general idea in two cases, which makes it a bit more precise.
For two variables the idea is pretty much the same, except that there is a full circle around a point. Then we have not just left or right, but all directions from all possible sides. For three or more variables it becomes impractical to visualise the paths as the domain itself is already in 3D and the function is in hyperspace.
Formal definition of a limit
The previous part was one step closer to a more precise definition of a limit. The basic idea relies on modulus, because we are dealing with distances between points which are infinitely close to zero. To calculate a limit for one point is fairly natural. It either converges to a value or not. Now, extend this same concept to each and every point of a function we get the concept that a function is continuous on each and every point of its domain. Most of the time in calculus our only concern with discontinuities are with division by zero, square roots of negative numbers or log of negative numbers. Most exercises on limits have just one point where the function is discontinuous.
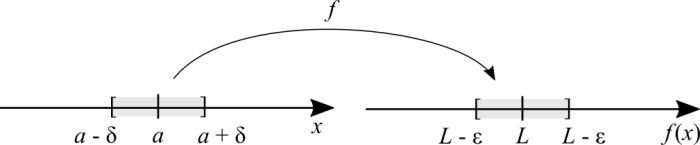
(The graph is not to scale, don't be fooled by thinking that [math]\displaystyle{ |L \pm \epsilon| = |a \pm \delta| \ !! }[/math])
First, the Greek letters [math]\displaystyle{ \delta }[/math] (lowercase delta) and [math]\displaystyle{ \epsilon }[/math] (epsilon). In physics, the letter [math]\displaystyle{ \Delta }[/math] (uppercase delta) is commonly used to denote distances or variations as in "average speed". The [math]\displaystyle{ \epsilon }[/math], for historical reasons, was associated to "error". In this case, the difference between two extremely close values of the function. [math]\displaystyle{ \delta }[/math] is a small distance from [math]\displaystyle{ a }[/math], to the right and to the left.
The reason for [math]\displaystyle{ L }[/math] at the graph rather than [math]\displaystyle{ f(a) }[/math] is that the function can be undefined there, yet the limit still exists. If [math]\displaystyle{ L = f(a) }[/math] then we could have written [math]\displaystyle{ f(a \pm \delta) }[/math] instead of [math]\displaystyle{ L \pm \epsilon }[/math]. But it could've been misleading in case [math]\displaystyle{ L \neq f(a) }[/math].
Let's take advantage of visualising the function's domain on the number line again. [math]\displaystyle{ a }[/math] is any point in the function's domain. [math]\displaystyle{ a \pm \delta }[/math] is the smallest step possible to the right or to the left of [math]\displaystyle{ a }[/math]. Conversely, [math]\displaystyle{ \epsilon }[/math] is the smallest possible error from [math]\displaystyle{ L }[/math]. Let's choose some [math]\displaystyle{ x }[/math] anywhere in that interval, with the exception of [math]\displaystyle{ x \neq a }[/math] because [math]\displaystyle{ f(a) }[/math] may not be defined. After we choose [math]\displaystyle{ x }[/math], [math]\displaystyle{ f(x) }[/math] "falls" anywhere in between [math]\displaystyle{ L \pm \epsilon }[/math], except for [math]\displaystyle{ f(a) }[/math]. The previous reasoning can be expressed with this notation:
[math]\displaystyle{ \text{if} \ 0 \lt |x - a| \lt \delta \implies |f(x) - L| \lt \epsilon }[/math]
Is the formal definition of a limit. No matter what [math]\displaystyle{ x }[/math] we choose, it's distance from [math]\displaystyle{ a }[/math] is never going to be zero nor greater than the smallest possible distance between two points. Conversely, the image that we calculate is never going to be at a distance greater than the the smallest possible distance between the limit and the function's value itself.
We can clearly see on the function's graph that the modulus, the distance between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], can also be written like this:
[math]\displaystyle{ \text{if} \ a - \delta \lt x \lt a + \delta \implies L - \epsilon \lt f(x) \lt L + \epsilon }[/math]
We've just applied one of the properties of the absolute value, this one: [math]\displaystyle{ |a| \lt b \iff -b \lt a \lt b }[/math].
Note: textbooks have this wording "given [math]\displaystyle{ \epsilon \gt 0 }[/math] there is a (or we have a) [math]\displaystyle{ \delta \gt 0 }[/math] such ...". I have to admit that it took me ages to finally understand why this was somewhat confusing. It's all related to the order that the definition shows it to us. When we learn about functions, there is the input or independent variable and the output or the dependent variable. The formal definition of a limit presents us with [math]\displaystyle{ \epsilon }[/math] first and then [math]\displaystyle{ \delta }[/math], which can be confusing in regards to the definition of dependent and independent variables. The definition says "given". How can it be given if [math]\displaystyle{ f(x) }[/math] depends on [math]\displaystyle{ x }[/math]? That's the confusion!
If you didn't quite grasp the idea of epsilon and delta, I'll try this: let's call epsilon a margin of error. Why does the definition give it? Assume that we have a margin of error of say, 1% (I'm resorting to statistical thinking). Say that the limit of a function is equal to 10 at [math]\displaystyle{ x = 5 }[/math]. A margin of error of 1% means that we are accepting values within the interval [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. Now to explain the delta. It is a number, very close to 5, such that if we calculate [math]\displaystyle{ f(5 \pm \delta) }[/math], the image is going to be somewhere within [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. In other words, it's a number such that, whatever value [math]\displaystyle{ f(5 \pm \delta) }[/math] assumes, it's never going to be greater than 10 + 1% or less than 10 - 1%.
Suppose now that we are given a margin of error that is exactly 0%. What does it mean in regards to a limit? It means that there is no difference between the calculated limit and the value of the function itself. The distance between the limit and the value of the function is zero, because one is equal to the other. We are either off by some margin of error from the true value or not, we can't be at a negative distance from it and this explains why epsilon is always positive. I hope this have cleared out the fog that covers this rather abstract definition.
Please do take note that I did all this explanation while considering a limit that is not infinite. When a limit exists and is a number, the function is said to be continuous there. Because if the limit exists but it's infinite, the function cannot be continuous there.
The squeeze theorem
If you look at the formal definition of a limit again, the boundaries to the left and to the right can very well be functions. That's the concept of this theorem. Any given point at the plane can have infinitely many functions passing there. In particular, we can put a function in between two others, essentially "crushing" it between the known values of the other two. Notice that the functions we put as boundaries has to have limits that converge to that point, if they are diverging to infinity it doesn't make sense. In spite of the graph depicting [math]\displaystyle{ h }[/math] above and [math]\displaystyle{ g }[/math] below, respectively, from [math]\displaystyle{ f }[/math], our only concern is at the neighbourhood of [math]\displaystyle{ x = a }[/math]. It's not required for [math]\displaystyle{ g }[/math] to always be below and [math]\displaystyle{ h }[/math] to always be above [math]\displaystyle{ f }[/math].
This theorem is required when intuition fails and we can't know for sure whether the function is converging or not to some value at some point.
[math]\displaystyle{ \text{if} \ g(x) \leq f(x) \leq h(x) }[/math] [math]\displaystyle{ \lim_{x \ \to \ a} g(x) = \lim_{x \ \to \ a} h(x) = L \implies \lim_{x \ \to \ a} f(x) = L }[/math]
The textbooks that I have don't show it, but if we extended to functions of two variables, we would have the same concept. Except that it's much harder to visualise in 3D.
Continuity in physics, economics and other fields
In a calculus course we are, for the most part, doing calculations with functions that may or may not represent any process. An interesting question is whether or not processes are continuous. Take velocity for instance. When something changes velocity from some value to another, it must be a process that smoothly covers all values in between. Now think about quantities which are always counted with integers: people, planets or the number of crimes. Half a person or half a planet doesn't exist. A crime either happens or not. This concept is usually discussed in statistics and there are cases where we can choose a variable to be either continuous our not depending on what we need. Age for example, 1 year old and 2 years old. We can count 1.5 years old and that depends on whether our experiment or model requires such values or not.
Regarding physics. For the most part, almost all theories that we learn in physics rely on the fact that units of space, time and mass (the fundamental units) are all continuous. We can subdivide without limits. When we get to discuss the meaning of say, 1 second divided by 1 trillion. Or what is it the mass of an atom divided by 1000? Then we reach philosophy. Money for example: we aren't concerned with quantities such as 1$ divided by 1000. Or interest rates, we aren't concerned with an interest rate of 1.0000000001%.
The concept of a discrete function is usually left for a course in statistics. In calculus we are mostly concerned with continuous processes and often using a continuous function is acceptable.