Formal limit and continuity of a single variable function
The discussion of two sided limits was one step closer to a more precise definition of a limit. The basic idea relies on modulus, because we are dealing with distances between points which are infinitely close to zero. To calculate a limit for one point is fairly natural. It either converges to a value or not. Now, extend this same concept to each and every point of a function we get the concept that a function is continuous on each and every point of its domain. Most of the time in calculus our only concern with discontinuities are with division by zero, square roots of negative numbers or log of negative numbers. Most exercises on limits have just one point where the function is discontinuous.
(The graph is not to scale, don't be fooled by thinking that [math]\displaystyle{ |L \pm \epsilon| = |a \pm \delta| \ !! }[/math])
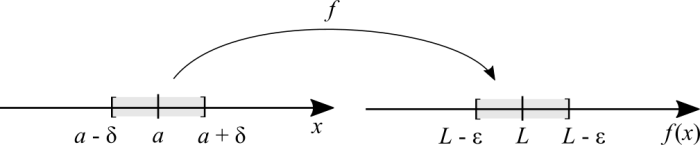
First, the Greek letters [math]\displaystyle{ \delta }[/math] (lowercase delta) and [math]\displaystyle{ \epsilon }[/math] (epsilon). In physics, the letter [math]\displaystyle{ \Delta }[/math] (uppercase delta) is commonly used to denote distances or variations as in "average speed". The [math]\displaystyle{ \epsilon }[/math], for historical reasons, was associated to "error". In this case, the difference between two extremely close values of the function. [math]\displaystyle{ \delta }[/math] is a small distance from [math]\displaystyle{ a }[/math], to the right and to the left.
The reason for [math]\displaystyle{ L }[/math] at the graph rather than [math]\displaystyle{ f(a) }[/math] is that the function can be undefined there, yet the limit still exists. If [math]\displaystyle{ L = f(a) }[/math] then we could have written [math]\displaystyle{ f(a \pm \delta) }[/math] instead of [math]\displaystyle{ L \pm \epsilon }[/math]. But it could've been misleading in case [math]\displaystyle{ L \neq f(a) }[/math].
Let's take advantage of visualising the function's domain on the number line again. [math]\displaystyle{ a }[/math] is any point in the function's domain. [math]\displaystyle{ a \pm \delta }[/math] is the smallest step possible to the right or to the left of [math]\displaystyle{ a }[/math]. Conversely, [math]\displaystyle{ \epsilon }[/math] is the smallest possible error from [math]\displaystyle{ L }[/math]. Let's choose some [math]\displaystyle{ x }[/math] anywhere in that interval, with the exception of [math]\displaystyle{ x \neq a }[/math] because [math]\displaystyle{ f(a) }[/math] may not be defined. After we choose [math]\displaystyle{ x }[/math], [math]\displaystyle{ f(x) }[/math] "falls" anywhere in between [math]\displaystyle{ L \pm \epsilon }[/math], except for [math]\displaystyle{ f(a) }[/math]. The previous reasoning can be expressed with this notation:
[math]\displaystyle{ \text{if} \ 0 \lt |x - a| \lt \delta \implies |f(x) - L| \lt \epsilon }[/math]
Is the formal definition of a limit. No matter what [math]\displaystyle{ x }[/math] we choose, it's distance from [math]\displaystyle{ a }[/math] is never going to be zero nor greater than the smallest possible distance between two points. Conversely, the image that we calculate is never going to be at a distance greater than the the smallest possible distance between the limit and the function's value itself.
We can clearly see on the function's graph that the modulus, the distance between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], can also be written like this:
[math]\displaystyle{ \text{if} \ a - \delta \lt x \lt a + \delta \implies L - \epsilon \lt f(x) \lt L + \epsilon }[/math]
We've just applied one of the properties of the absolute value, this one: [math]\displaystyle{ |a| \lt b \iff -b \lt a \lt b }[/math].
Note: textbooks have this wording "given [math]\displaystyle{ \epsilon \gt 0 }[/math] there is a (or we have a) [math]\displaystyle{ \delta \gt 0 }[/math] such ...". I have to admit that it took me ages to finally understand why this was somewhat confusing. Suppose an exercise gives you a function representing Velocity x Time. If we know the function or the graph and we are given [math]\displaystyle{ t = x \ s }[/math], then we can find velocity because we are given the time. The formal definition of a limit says that we are given an epsilon which is the error from the limit and a nearby [math]\displaystyle{ f(x) }[/math]. With the function being continuous, then we can always find a delta such that calculating the function for that delta is going to yield a value that is nearby the function's limit. No matter how small epsilon is, there is going to be a corresponding delta for it. The idea of a limit is that we can always find a number that, calculating [math]\displaystyle{ f(x) }[/math], the result is nearby the limit. In the same way velocity depends on time, delta depends on epsilon.
If you didn't quite grasp the idea of epsilon and delta, I'll try this: let's call epsilon a margin of error. Assume that we have a margin of error of say, 1% (I'm resorting to statistical thinking). Say that the limit of a function is equal to 10 at [math]\displaystyle{ x = 5 }[/math]. A margin of error of 1% means that we are accepting values within the interval [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. Now to explain the delta. It is a number, very close to 5, such that if we calculate [math]\displaystyle{ f(5 \pm \delta) }[/math], the image is going to be somewhere within [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. In other words, it's a number such that, whatever value [math]\displaystyle{ f(5 \pm \delta) }[/math] assumes, it's never going to be greater than 10 + 1% or less than 10 - 1%. We can reduce the margin of error to 0.1%, to 0.01% and beyond, indefinitely. There is going to be a number close to 5 such that we calculate the function for that number are we are still somewhere in between the margin of error.
The definition is rather abstract because it deals with a concept that is the infinitely close to a number. [math]\displaystyle{ \epsilon }[/math] represents the smallest possible error, the distance between the true value and some approximation of it. [math]\displaystyle{ \delta }[/math] represents some number, such that calculating the function for that number should yield a value that is also close to the theoretical limit of the function. Notice that the margin of error has to be positive. It doesn't make sense for it to be negative because either you are off the true value by some positive distance or the distance is zero and the error is zero. I hope this have cleared out the fog that covers this rather abstract definition.
Please do take note that I did all this explanation while considering a limit that is not infinite. When a limit exists and is a number, the function is said to be continuous there. Because if the limit exists but it's infinite, the function cannot be continuous there.
The squeeze theorem
If you look at the formal definition of a limit again, the boundaries to the left and to the right can very well be functions. That's the concept of this theorem. Any given point at the plane can have infinitely many functions passing there. In particular, we can put a function in between two others, essentially "crushing" it between the known values of the other two. Notice that the functions we put as boundaries has to have limits that converge to that point, if they are diverging to infinity it doesn't make sense. In spite of the graph depicting [math]\displaystyle{ h }[/math] above and [math]\displaystyle{ g }[/math] below, respectively, from [math]\displaystyle{ f }[/math], our only concern is at the neighbourhood of [math]\displaystyle{ x = a }[/math]. It's not required for [math]\displaystyle{ g }[/math] to always be below and [math]\displaystyle{ h }[/math] to always be above [math]\displaystyle{ f }[/math].
This theorem is required when intuition fails and we can't know for sure whether the function is converging or not to some value at some point.
[math]\displaystyle{ \text{if} \ g(x) \leq f(x) \leq h(x) }[/math] [math]\displaystyle{ \lim_{x \ \to \ a} g(x) = \lim_{x \ \to \ a} h(x) = L \implies \lim_{x \ \to \ a} f(x) = L }[/math]
The textbooks that I have don't show it, but if we extended to functions of two variables, we would have the same concept. Except that it's much harder to visualise in 3D.
Continuity in physics, economics and other fields
In a calculus course we are, for the most part, doing calculations with functions that may or may not represent any process. An interesting question is whether or not processes are continuous. Take velocity for instance. When something changes velocity from some value to another, it must be a process that smoothly covers all values in between. Now think about quantities which are always counted with integers: people, planets or the number of crimes. Half a person or half a planet doesn't exist. A crime either happens or not. This concept is usually discussed in statistics and there are cases where we can choose a variable to be either continuous our not depending on what we need. Age for example, 1 year old and 2 years old. We can count 1.5 years old and that depends on whether our experiment or model requires such values or not.
Regarding physics. For the most part, almost all theories that we learn in physics rely on the fact that units of space, time and mass (the fundamental units) are all continuous. We can subdivide without limits. When we get to discuss the meaning of say, 1 second divided by 1 trillion. Or what is it the mass of an atom divided by 1000? Then we reach philosophy. Money for example: we aren't concerned with quantities such as 1$ divided by 1000. Or interest rates, we aren't concerned with an interest rate of 1.0000000001%.
The concept of a discrete function is usually left for a course in statistics. In calculus we are mostly concerned with continuous processes and often using a continuous function is acceptable.