Formal limit and continuity of a single variable function

The discussion of two sided limits was one step closer to a more precise definition of a limit. The basic idea relies on modulus, because we are dealing with distances between points which are infinitely close to zero. To calculate a limit for one point is fairly natural. It either converges to a value or not. Now, extend this same concept to each and every point of a function we get the concept that a function is continuous on each and every point of its domain. Most of the time in calculus our only concern with discontinuities are with division by zero, square roots of negative numbers or log of negative numbers. Most exercises on limits have just one point where the function is discontinuous.

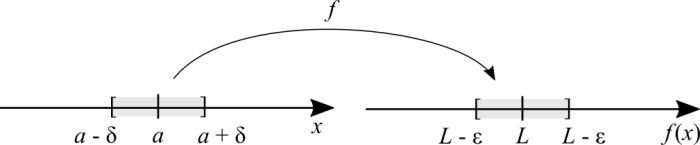
(The graph is not to scale, don't be fooled by thinking that [math]\displaystyle{ |L \pm \epsilon| = |a \pm \delta| \ !! }[/math])

First, the Greek letters [math]\displaystyle{ \delta }[/math] (lowercase delta) and [math]\displaystyle{ \epsilon }[/math] (epsilon). In physics, the letter [math]\displaystyle{ \Delta }[/math] (uppercase delta) is commonly used to denote distances or variations as in "average speed". The [math]\displaystyle{ \epsilon }[/math], for historical reasons, was associated to "error". In this case, the difference between two extremely close values of the function. [math]\displaystyle{ \delta }[/math] is a small distance from [math]\displaystyle{ a }[/math], to the right and to the left.

The reason for [math]\displaystyle{ L }[/math] at the graph rather than [math]\displaystyle{ f(a) }[/math] is that the function can be undefined there, yet the limit still exists. If [math]\displaystyle{ L = f(a) }[/math] then we could have written [math]\displaystyle{ f(a \pm \delta) }[/math] instead of [math]\displaystyle{ L \pm \epsilon }[/math]. But it could've been misleading in case [math]\displaystyle{ L \neq f(a) }[/math].

Let's take advantage of visualising the function's domain on the number line again. [math]\displaystyle{ a }[/math] is any point in the function's domain. [math]\displaystyle{ a \pm \delta }[/math] is the smallest step possible to the right or to the left of [math]\displaystyle{ a }[/math]. Conversely, [math]\displaystyle{ \epsilon }[/math] is the smallest possible error from [math]\displaystyle{ L }[/math]. Let's choose some [math]\displaystyle{ x }[/math] anywhere in that interval, with the exception of [math]\displaystyle{ x \neq a }[/math] because [math]\displaystyle{ f(a) }[/math] may not be defined. After we choose [math]\displaystyle{ x }[/math], [math]\displaystyle{ f(x) }[/math] "falls" anywhere in between [math]\displaystyle{ L \pm \epsilon }[/math], except for [math]\displaystyle{ f(a) }[/math]. The previous reasoning can be expressed with this notation:

[math]\displaystyle{ \text{if} \ 0 \lt |x - a| \lt \delta \implies |f(x) - L| \lt \epsilon }[/math]

Is the formal definition of a limit. The distance between the function's image and the limit can be made infinitely small. We choose a point such that calculating the function for it is going to be close to the limit. The distance between that point and the point at which we have the limit can be made infinitely small.

We can clearly see on the function's graph that the modulus, the distance between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], can also be written like this:

[math]\displaystyle{ \text{if} \ a - \delta \lt x \lt a + \delta \implies L - \epsilon \lt f(x) \lt L + \epsilon }[/math]

We've just applied one of the properties of the absolute value, this one: [math]\displaystyle{ |a| \lt b \iff -b \lt a \lt b }[/math].

Note: textbooks have this wording "given [math]\displaystyle{ \epsilon \gt 0 }[/math] there is a (or we have a) [math]\displaystyle{ \delta \gt 0 }[/math] such ...". I have to admit that it took me ages to finally understand why this was somewhat confusing. Suppose an exercise gives you a function representing Velocity x Time. If we know the function or the graph and we are given [math]\displaystyle{ t = x \ s }[/math], then we can find velocity because we are given the time. The formal definition of a limit says that we are given an epsilon which is the error from the limit and a nearby [math]\displaystyle{ f(x) }[/math]. With the function being continuous, then we can always find a delta such that calculating the function for that delta is going to yield a value that is nearby the function's limit. Else, if it isn't nearby, the limit doesn't exist. No matter how small epsilon is, there is going to be a corresponding delta for it. In the same way velocity depends on time, delta depends on epsilon.

If you didn't quite grasp the idea of epsilon and delta, I'll try this: let's call epsilon a margin of error. Assume that we have a margin of error of say, 1% (I'm resorting to statistical thinking). Say that the limit of a function is equal to 10 at [math]\displaystyle{ x = 5 }[/math]. A margin of error of 1% means that we are accepting values within the interval [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. Now to explain the delta. It is a number, very close to 5, such that if we calculate [math]\displaystyle{ f(5 \pm \delta) }[/math], the image is going to be somewhere within [math]\displaystyle{ [10 - 1%, 10 + 1%] }[/math]. In other words, it's a number such that, whatever value [math]\displaystyle{ f(5 \pm \delta) }[/math] assumes, it's never going to be greater than 10 + 1% or less than 10 - 1%. We can reduce the margin of error to 0.1%, to 0.01% and beyond, indefinitely. There is going to be a number close to 5 such that we calculate the function for that number are we are still somewhere in between the margin of error.

The definition is rather abstract because it deals with a concept that is the infinitely close to a number. [math]\displaystyle{ \epsilon }[/math] represents the smallest possible error, the distance between the true value and some approximation of it. [math]\displaystyle{ \delta }[/math] represents some number, such that calculating the function for that number should yield a value that is also close to the theoretical limit of the function. Notice that the margin of error has to be positive. It doesn't make sense for it to be negative because either you are off the true value by some positive distance or the distance is zero and the error is zero. I hope this have cleared out the fog that covers this rather abstract definition.

Please do take note that I did all this explanation while considering a limit that is not infinite. When a limit exists and is a number, the function is said to be continuous there. Because if the limit exists but it's infinite, the function cannot be continuous there.

Formal definition of continuity

Before giving it I shall discuss a problem. Suppose we have a function [math]\displaystyle{ f }[/math] that is defined as equal to 100 (I'm using 100 just to make it clear that there is a huge gap) if the dependent variable is a rational number, 0 if the dependent variable is irrational. Let's see what happens if we try to calculate the sided limits. Let's suppose that [math]\displaystyle{ a }[/math] is rational, then [math]\displaystyle{ f(a) = 100 }[/math].

[math]\displaystyle{ \lim_{x \ \to \ a^{+}}f(x) }[/math]. Now [math]\displaystyle{ a + \delta }[/math], with [math]\displaystyle{ \delta }[/math] being rational the sum yields a rational number. In between it and [math]\displaystyle{ a }[/math] there is an irrational because there is a theorem that states this. But the function is defined as 0 for irrational numbers. The limit won't be 100 then. Now if [math]\displaystyle{ \delta }[/math] is irrational, the sum is irrational. In between an irrational and a rational there can't be a number that is both irrational and rational at the same time. We have a contradiction here. As we approach [math]\displaystyle{ a }[/math] from the right the limit can't be both 0 and 100 at the same time. Repeat for the left side and the same problem. The conclusion is that the function is defined for all reals, but the limit won't exist anywhere. Hence, this function is discontinuous everywhere.

For each [math]\displaystyle{ \epsilon }[/math] given, there is a [math]\displaystyle{ \delta \gt 0 }[/math] ([math]\displaystyle{ \delta }[/math] depends on [math]\displaystyle{ \epsilon }[/math]), such that [math]\displaystyle{ f(x) }[/math] is bounded by [math]\displaystyle{ f(a) - \epsilon }[/math] and [math]\displaystyle{ f(a) + \epsilon }[/math]. While [math]\displaystyle{ x }[/math] is bounded by [math]\displaystyle{ a - \delta }[/math] and [math]\displaystyle{ a + \delta }[/math]. With [math]\displaystyle{ x }[/math] belonging to the function's domain.

The difference between this and the formal definition of a limit is that in here we want the limit to be equal to a point in the function's graph. In the formal definition we are looking for the existence on the limit itself, which may or may not coincide with a point in the function's graph.

The squeeze theorem

If you look at the formal definition of a limit again, the boundaries to the left and to the right can very well be functions. That's the concept of this theorem. Any given point at the plane can have infinitely many functions passing there. In particular, we can put a function in between two others, essentially "crushing" it between the known values of the other two. Notice that the functions we put as boundaries has to have limits that converge to that point, if they are diverging to infinity it doesn't make sense. In spite of the graph depicting [math]\displaystyle{ h }[/math] above and [math]\displaystyle{ g }[/math] below, respectively, from [math]\displaystyle{ f }[/math], our only concern is at the neighbourhood of [math]\displaystyle{ x = a }[/math]. It's not required for [math]\displaystyle{ g }[/math] to always be below and [math]\displaystyle{ h }[/math] to always be above [math]\displaystyle{ f }[/math].

This theorem is required when intuition fails and we can't know for sure whether the function is converging or not to some value at some point.

[math]\displaystyle{ \text{if} \ g(x) \leq f(x) \leq h(x) }[/math] [math]\displaystyle{ \lim_{x \ \to \ a} g(x) = \lim_{x \ \to \ a} h(x) = L \implies \lim_{x \ \to \ a} f(x) = L }[/math]

The textbooks that I have don't show it, but if we extended to functions of two variables, we would have the same concept. Except that it's much harder to visualise in 3D.