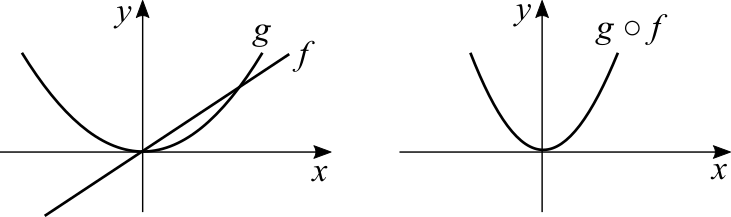Chain rule for single variable functions
The chain rule is, intuitively, a product of two derivatives. Suppose that we have a person walking at a speed of 1 m/s. Now suppose we have a train moving at 20 m/s in the same direction as the person. The train is obviously 20x faster than the walking person, if we are measuring in respect to the static ground. Now imagine that the person is walking at 1 m/s while inside the train moving at 20 m/s. What's the the person's velocity? We have a physics problem here, because it really depends on whether we want velocity in respect to the ground or to the train.
From the point of view of mathematics we have a composite function to describe the previously mentioned motion: position in respect to time. Because the person's velocity is a ratio space / time and for each unit of it, the train is also moving in the same direction. In other words, we have a product of ratios. That's precisely the idea of the chain rule when written with the Leibniz's notation:
[math]\displaystyle{ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} }[/math]
The definition of a function states that we have one variable that depends upon another. In the case of composite functions, the value of one function depends on the value of the other function. Extending it to rates of change and the rate of change of one function depends on the rate of change of the other function. That's why we have that [math]\displaystyle{ h(x) = f(g(x)) }[/math]:
[math]\displaystyle{ h'(x) = g'(x) \cdot f'(g(x)) }[/math]
We can have any number of functions nested within another. The rule still holds and the name comes from the fact that we have a chain of operations, a chain of derivatives. I think that the most common mistake with the chain rule is to derive the nested function twice, like this [math]\displaystyle{ g'(x)f'(g'(x)) }[/math]. One way to avoid this common mistake is to remember that we have a product of derivatives, not a composition of derivatives.
Note: sometimes we have a composition function but we don't see it clearly. For example: [math]\displaystyle{ y = \sin(x)^2 }[/math]. We can see that we have a product [math]\displaystyle{ y = \sin(x) \sin(x) }[/math], but we could also see it as [math]\displaystyle{ y = x^2 }[/math] and [math]\displaystyle{ x = sin(x) }[/math].
Graphical reasoning for the chain rule
I don't know about textbooks that show a graphical interpretation for the chain rule. Let's consider [math]\displaystyle{ f(x) = 3x }[/math] and [math]\displaystyle{ g(x) = x^2 }[/math]. The graph of the former is a straight line and the constant factor is the angular coefficient, greater meaning a stepper inclination. The latter is a parabola. The first has a constant rate of change, the second does not.
The graph of [math]\displaystyle{ g(f(x)) = (3x)^2 }[/math] has a greater rate of change than the graph of [math]\displaystyle{ g(x) = x^2 }[/math]. Think about this: if we choose [math]\displaystyle{ x = 2 }[/math] the rates of change are, at that point and for each function, [math]\displaystyle{ f'(2) = 6 }[/math] and [math]\displaystyle{ g'(2) = 4 }[/math]. For the composite function we have [math]\displaystyle{ g'(f(x)) = f'(2)g'(f(2)) = 6 \cdot 2 \cdot 3 = 36 }[/math]. I did this simple example with positive numbers but the chain rule holds for negative numbers and for more complicated functions.
Note: in this specific case we could have used the product rule. Or even faster, the power rule.
Proof of the chain rule
It's natural to think that the derivative of the composite function is the composition of the derivatives. It's the same intuition that commonly happens with the product and quotient rules. When we have a composition, one function is the dependent variable of the other. We can be easily fooled and think that the derivative of [math]\displaystyle{ f(g(x)) }[/math] is [math]\displaystyle{ f'(g'(x)) }[/math]. Mathematically this doesn't make sense because we just swapped a function by its derivative. Who said that it's right to replace a function by its derivative and expect the result of this operation to be meaningful? Who said that the rate of change of [math]\displaystyle{ f }[/math] depends on the rate of change of [math]\displaystyle{ g }[/math]? Think about this: if a function represents velocity in respect to time, its derivative is acceleration in respect to time. There is no meaning in "derive time in respect to (what)?" In this case time is not even dependent on anything to begin with.
The problem of finding the tangent line describes how a differentiable function can be seen as a linear function if we consider a small enough interval around a point. Let's begin by defining two affine functions:
[math]\displaystyle{ f(x) = ax + b }[/math]
[math]\displaystyle{ g(x) = cx + d }[/math]
Let's take a look at:
[math]\displaystyle{ f(g(x)) = ag(x) + b }[/math]
[math]\displaystyle{ f(cx + d) = a(cx + d) + b }[/math]
[math]\displaystyle{ f \circ g = acx + ad + b }[/math]
Did you notice the product between the angular coefficients, [math]\displaystyle{ a \cdot c }[/math]? If we differentiate the expression [math]\displaystyle{ acx + ad + b }[/math] in respect to [math]\displaystyle{ x }[/math], the operation yields [math]\displaystyle{ ac }[/math]! Surprise! That's not a formal proof though. Let's see what happens if we rewrite the same reasoning with linear approximations in mind: