Finding critical points of a single variable function

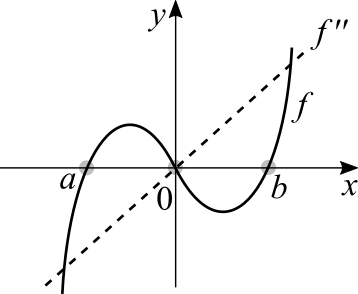
This part continues from where maximum and minimum points of a function left off. Now we deal with the specific case of [math]\displaystyle{ f''(x) = 0 }[/math]. In the same way the derivative shows us whether a function is crescent or decrescent in a certain interval, the second derivative does the same for the derivative itself. With the second derivative we know whether a function's rate of change is increasing or decreasing over time, which graphically means that the function's concavity (its curvature) is either upwards or downwards. Let's inspect the graph of a cubic and its second derivative:

[math]\displaystyle{ ]a, \ 0[ }[/math] we have that [math]\displaystyle{ f''(x) \lt 0 }[/math]. The second derivative is crescent, its sign is negative and the graph of [math]\displaystyle{ f }[/math] is a downwards parabola.

[math]\displaystyle{ ]0, \ b[ }[/math] we have that [math]\displaystyle{ f''(x) \gt 0 }[/math]. The second derivative is crescent, its sign is positive and the graph of [math]\displaystyle{ f }[/math] is an upwards parabola.

At the origin [math]\displaystyle{ f''(x) = 0 }[/math]. When [math]\displaystyle{ f'(x) = 0 }[/math] it means that we have a horizontal tangent line at that point. When [math]\displaystyle{ f''(x) = 0 }[/math] it means that the derivative has changed from crescent to decrescent or vice-versa. It's called an inflection point, the point where [math]\displaystyle{ f }[/math] inverts its rate of change from positive to negative or vice-versa. Which is exactly what we see in the graph.

Careful! In the same way the derivative's root may or may not coincide with a local maximum or minimum, the second derivative's root may or may not coincide with the root of a function.