Defining the gradient
To properly understand the gradient one is required to know vectors and the dot (or scalar) product. When we have color gradients what we see is that one extreme has one color and the other extreme another color, in between a gradient that is the transition between one color to the other. In physics there exists many types of gradients, such as gradients of temperature or pressure. Gradients are important because there are certain phenomena that require strong gradients to happen, such as there is no wind or oceanic currents if there is no pressure gradient between two points. Conceptually we have some quantity that changes in intensity over space and with a particular direction. That's the gradient.
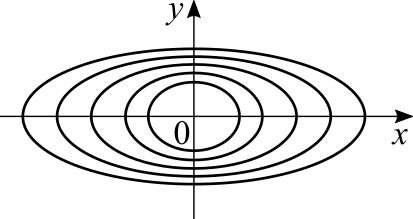
Before going on for a mathematical definition, let's look at a graph of level curves:
The rate of change over the [math]\displaystyle{ x }[/math] axis is less than over the [math]\displaystyle{ y }[/math] axis because the level curves are closer in the latter direction than on the former. If we walk along the same level we don't experience any changes in the value of [math]\displaystyle{ f(x,y) }[/math], which means that the rate of change is zero for directions parallel to a level curve. The highest rates of change are achieved when we move perpendicularly to the level curves, which is the shortest path between them. If the distance between two consecutive level curves is close to zero, it means that the function's slope is close to 90°. Otherwise, if the distance between them tends to infinity, then the slope is close to 0°.
[math]\displaystyle{ D_xf \cdot a + D_yf \cdot b }[/math]. Taking a second look at the directional derivative notice that we have a sum of terms where each one is a product between the coordinates of the vector given and the partial derivatives for that coordinate. That formula is a dot product. Conclusion? We have two vectors in it, one is the vector that gives the direction which we want to find the rate of change on, the other is
[math]\displaystyle{ \nabla f = \left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right) }[/math]
For [math]\displaystyle{ n }[/math] variables we have a gradient with [math]\displaystyle{ n }[/math] coordinates. The flipped Delta is the letter Nabla, read it "del [math]\displaystyle{ f }[/math]".
We can rewrite the directional derivative using the gradient as follows
[math]\displaystyle{ \frac{\partial f}{\partial \overrightarrow{v}}(a,b) = \left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right) \cdot (a,b) = \nabla f \cdot \overrightarrow{v} }[/math]
Which direction is tangent and which direction is perpendicular?
With graphs of functions of two variables it may be difficult to see which direction is perpendicular and which is tangent to a certain point. With graphs of functions of one variable there is only one angular coefficient per point. With graphs in 3D there is the z axis and two angles, one for z and another for xy. Recall that partial derivatives give a rate of change that is parallel to the axis. With this in mind the gradient vector is parallel to the XY plane in the case of [math]\displaystyle{ \nabla f (x,y) }[/math].
Let's see a graphical example with the function [math]\displaystyle{ f(x,y) = x^2 + y^2 }[/math] and the level curve for [math]\displaystyle{ f(x,y) = 2 }[/math]. Gradient is [math]\displaystyle{ \nabla f = (2x, 2y) }[/math]. Now we apply the points [math]\displaystyle{ (1, 0) }[/math], [math]\displaystyle{ (0, 1) }[/math] and [math]\displaystyle{ (1, 1) }[/math]:
It shouldn't be a surprise that the gradient vectors are perpendicular to the level curves and on the same plane as them. Along a level curve the function has the same constant value. In which direction the function changes from one value to another? From one level curve to another, which is perpendicular to a level curve. The gradient is also not a single vector, but a whole field of vectors. It's a function that outputs vectors.