Properties of roots

The association of square roots with squares is natural. Cubic roots are associated with cubes and there isn't much complexity to it. With higher dimensions we lose the geometric visualisation and have to rely on numbers alone.

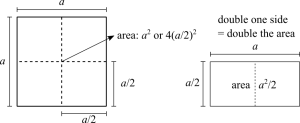
The relationship between [math]\displaystyle{ a^2 }[/math] and [math]\displaystyle{ \sqrt{a} }[/math] is the same as exponential and logarithm. One is the inverse of the other. Every time we have a number to the power of two, it means the area of a square with the length of each side side equal to that number. The square root finds the length of a side of a square, for which its square is the area of that square. I think this is were two confusions happen: one is to think that the square root is halving the number. No! It's halving the sides of a square. The other is that, when we double the length of each side, the area of the square is quadrupled. The reverse process, the square root, results in a square with an area that is 1/4 of the original one. With that in mind one may think that square root is the same as to divide by 4. (using a bit of imagination a square has four sides!)

The previously mentioned confusion is specially common with physics. Because when we have units that are squared such as [math]\displaystyle{ m^2 }[/math] and [math]\displaystyle{ m/s^2 }[/math], a lot of interpretation mistakes originate from there.

• [math]\displaystyle{ \sqrt{a} + \sqrt{b} \neq \sqrt{a \ + \ b} \iff a^2 + b^2 \neq (a + b)^2 }[/math]. Assuming that [math]\displaystyle{ a,b \neq 0 }[/math]. The sum of roots is not the root of the sum. Conversely, the sum of squares is not the square of the sum (except for [math]\displaystyle{ a = b = 1 \ \text{or} \ -1 }[/math]). It's easy to see it with squares. One very common application of this is resolution of screens, monitors and photos. If we have two monitors with the same resolution each, we didn't square the resolution, we doubled it. This is also a way to explain that increasingth the length or width of a terrain does increase the total area, but much less than increasing both dimensions at the same time. This is the same informal reasoning to explain why increasing a circle's or sphere's radius has the effect of increasing the circle's perimeter or the sphere's surface much less than the circle's area or the volume of a sphere.