Diferenciação implícita

Uma função definida explicitamente tem a forma [math]\displaystyle{ y = f(x) }[/math], tal como [math]\displaystyle{ f(x) = x^2 + 2 }[/math]. Uma função definida implicitamente não apresenta as variáveis direitinho à direita e à esquerda. Por exemplo: [math]\displaystyle{ x^2 + y^2 = 4 }[/math]. Esta não é uma equação de uma função. Ela descreve uma circunferência de acordo com a geometria analítica. Porém, ela "esconde" uma função. Podemos isolar [math]\displaystyle{ y }[/math] para obter [math]\displaystyle{ y = \pm \sqrt{x^2 + 1} }[/math]. Como a circunferência é simétrica em todas as direções poderíamos ter isolado o [math]\displaystyle{ x }[/math] para obter a mesma equação, exceto que as variáveis estariam trocadas.

Para equações complicadas como [math]\displaystyle{ y^3 + x^2y^2 + 4x = 0 }[/math] podemos tentar, mas vai ser praticamente impossível de conseguir isolar uma variável e achar a função explícita. Uma forma gráfica de interpretar tais equações é pensar nelas em termos de geometria analítica. Quantos pares [math]\displaystyle{ (x, \ y) }[/math] satisfazem a equação mencionada anteriormente? Infinitos, é uma equação que em 2D descreve alguma curva ou caminho. Da mesma forma que podemos traçar funções ponto por ponto e ligando-os por linhas retas, uma curva complicada também pode ser aproximada com a mesma técnica.

A curva dada anteriormente poderia ser reescrita assim [math]\displaystyle{ [f(x)]^3 + x^2[f(x)]^2 + 4x = 0 }[/math] se lembrarmos que [math]\displaystyle{ y = f(x) }[/math]. Aí esta a nossa função desconhecida. A substituição deixou claro que existe uma relação entre as duas variáveis da equação. Com cálculo não podemos resolver a equação e provavelmente há muitas funções que satisfariam a equação. O que podemos fazer é achar [math]\displaystyle{ f'(x) }[/math] e com isto ter uma ideia melhor da forma da curva.

O mesmo raciocínio pode ser estendido para funções de várias variáveis.

Discussão prática com gráficos

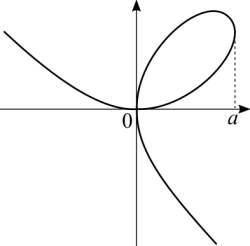
A discussão anterior pode ter sido abstrata demais. Vamos discutir a Folium de Descartes:

[math]\displaystyle{ x^3 + y^3 = 3xy }[/math]

O gráfico pode ser descrito por uma função, mas ela terá que ser por partes (ramos em Portugal). Para o intervalo [math]\displaystyle{ [0,a] }[/math] temos que um certo [math]\displaystyle{ x }[/math] pode corresponder a até três valores diferentes de [math]\displaystyle{ y }[/math]. Isto significa que naquele intervalo há até três funções diferentes. Faz todo sentido porque a equação tem um termo [math]\displaystyle{ y^3 }[/math] que aceita até três valores.

Se pensarmos na função que pode traçar o gráfico e o problema de achar a reta tangente num dado ponto, temos que pensar em [math]\displaystyle{ y' = f'(x) }[/math]. Temos uma equação e diferenciamos ambos os lados em relação à mesma variável. Na notação de Leibniz:

[math]\displaystyle{ \frac{d}{dx}x^3 + \frac{d}{dx}y^3 = \frac{d}{dx}(3xy) }[/math]	Já começamos com a propriedade da soma de derivadas.
[math]\displaystyle{ 3x^2 + \frac{d}{dx}y^3 = 3y + 3x\frac{dy}{dx} }[/math]	A primeira derivada é fácil. O lado direito é um produto de duas funções. [math]\displaystyle{ 3x }[/math] é explícito e [math]\displaystyle{ y }[/math] é alguma função desconhecida. Portanto, use a regra do produto. Não confunda com derivadas parciais.
[math]\displaystyle{ 3x^2 + 3y^2\frac{dy}{dx} = 3y + 3x\frac{dy}{dx} }[/math]	[math]\displaystyle{ y^3 }[/math] não é [math]\displaystyle{ f(y) = y^3 }[/math], o que realmente temos é uma composição de uma função que é uma cúbica e outra função desconhecida, a que estamos tentando diferenciar. Se você não entendeu direito tente isto [math]\displaystyle{ f(x) = x^3 }[/math]. [math]\displaystyle{ g(x) = \ ? }[/math]. Então [math]\displaystyle{ g(x^3) = \ ??? }[/math]. Não conhecemos [math]\displaystyle{ g }[/math] mas isto não nos impede de saber derivar [math]\displaystyle{ f }[/math]. [math]\displaystyle{ (g \circ f)' = f'(x)g'(f(x)) = 3x^2g'(x^3) }[/math].
[math]\displaystyle{ x^2 + y^2\frac{dy}{dx} = y + x\frac{dy}{dx} }[/math]	Divida tudo por 3.
[math]\displaystyle{ y^2\frac{dy}{dx} - x\frac{dy}{dx} = y - x^2 }[/math]	Colocando as derivadas à esquerda.
[math]\displaystyle{ \frac{dy}{dx}(y^2 - x) = y - x^2 }[/math]	Ponha a derivada em evidência.
[math]\displaystyle{ \frac{dy}{dx} = \frac{y - x^2}{y^2 - x} }[/math]	Não estamos considerando a origem.